1. по заданным координатам (таблица 1, стр.17) построить проекции треугольника abc.
2. через точку в задать плоскость, перпендикулярную к стороне ас.
3. построить линию пересечения плоскости треугольника с перпендикулярной плоскостью.
4. определить видимость.
рекомендации к выполнению
пересечение двух плоскостей задает пространственную прямую. любую прямую можно построить по двум точкам, проводя ее непосредственно в одной из плоскостей. считается решенной, если удалось найти две конкретные точки прямой, лежащей в пересечении плоскостей.
искомую плоскость, перпендикулярную к прямой ас, целесообразно задать главными линиями плоскости – горизонталью h и фронталью f, перпендикулярных к прямой ас. секторы плоскости на п2 и п1 ограничить волнистой линией. точка в – общая для обеих плоскостей. вторую точку, принадлежащую обеим плоскостям, определяем с плоскости уровня q (q2) // п1, которая пересекает обе плоскости по горизонталям h/ и h//. на пересечении этих горизонталей находим вторую точку, (например, точку м). следовательно: вм – линия пересечения плоскостей. видимость определяем методом конкурирующих точек, которые должны принадлежать ас и h, ac и f.
при обводке чертежа необходимо соблюдать следующие цвета: данное по условию – черным цветом, построения – синим или зеленым цветом, искомые величины – красным цветом. все линии построения, обо¬значения на чертеже должны быть сохранены.
масштаб 1: 1.
(нужен алгоритм)
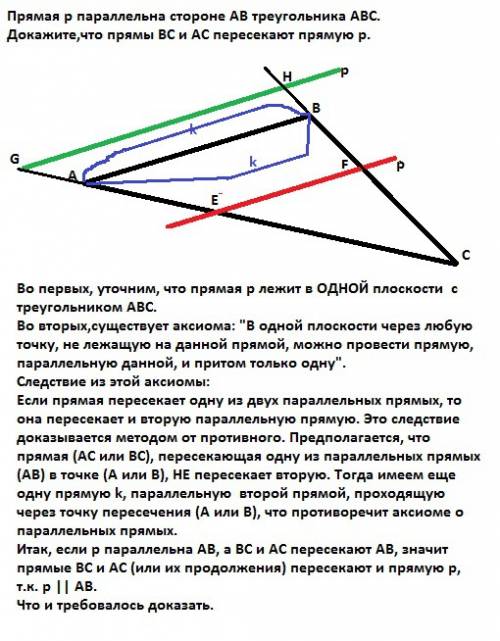
Во вторых,существует аксиома: "В одной плоскости через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну".
Следствие из этой аксиомы:
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую. Это следствие доказывается методом от противного.
Предполагается, что прямая (АС или ВС), пересекающая одну из параллельных прямых (АВ) в точке (А или В), НЕ пересекает вторую. Тогда имеем еще одну прямую k, параллельную второй прямой р, проходящую через точку пересечения (А или В), что противоречит аксиоме о параллельных прямых.
Итак, если p параллельна AB, а BC и АС пересекают AB, значит прямые BC и АС (или их продолжения) пересекают и прямую p, т.к. p || AB.