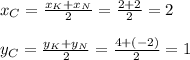
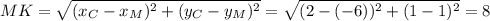

Отметим ромб буквами - левая верщина А, сверху В, справа С и внизу D.
Тогда треугольник АВС равнобедренный, т.к. это ромб, в котором все стороны равны. Значит, если угол ВАС = 32 градуса, то и угол ВСА = 32 градуса. Тогда в треугольнике ВОС (он кстати прямоугольный, т.к. диагонали ромба пересекаются под прямым углом) у нас уже есть два угла - угол ВОС = 90 градусов, угол ВСА = 32 градусам. Т.к. сумма углов в любом треугольнике равна 180 градусов, то в нашем треугольнике ВОС угол СВО = 180 - (90 + 32) = 180 - 122 = 58 градусов
MD = 2x
AD = 5x
h --высота параллелограмма
S(ABM) = (1/2)*AM*h = (1/2)*3x*h
S(MCD) = (1/2)*MD*h = (1/2)*2x*h
Sпараллелограмма = AD*h = 5x*h = 60
x*h = 12
S(ABM) = (1/2)*3*(x*h) = (1/2)*3*12 = 3*6 = 18 (см²)