ответ: Объем шарового сегмента опущенного в цилиндр = π*468 см³
Объяснение: Дано:
Диаметр шара = 30 см тогда его радиус R = 15
Радиус основания цилиндра r = 12см
Найти объем шарового сегмента, опушенного в цилиндр V - ?
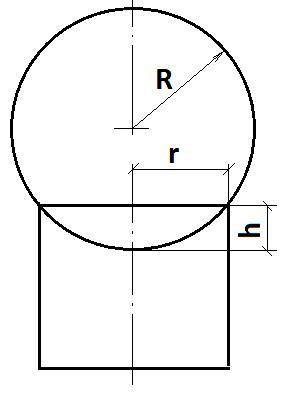
Смотрите рисунок. Что бы найти объем надо найти размер h - глубину погружения шара. По теореме Пифагора R² = r² + (R-h)² Получили квадратное уравнение: h² - 2Rh + r² = 0
h1,2 = (2R+-√4R² - 4r²)/2 = (2R+-2√R²-r²)/2 h = 6 см
Объем шарового сегмента найдем по формуле V = π*h²(R - h/3) = π*468 см³
Задача на подобие треугольников. Не буду повторяться, полное решение дано во вложенном рисунке к задаче, так легче рассматривать его ( когда все на одной странице)
Треугольники подобны по двум углам: вертикальному и образованному пересечением диагональю параллельных сторон параллелограмма. ( Прямые углы идут уже как третьи)
В записи решения не пояснила, откуда взялись 5 и 11 в уравнениях.
5=(2+3 ) сумма отношений отрезков меньшей диагонали,
11 = (3+8 ) сумма отношений отрезков большей диагоналию В рисунке они выполняют роль больших катетов получившихся треугольников.