1) Прямая КЕ и радиус, опущенный к точке К, образует прямой угол, выходит, что треугольник ЕОК прямоугольный и тогда сторону ОЕ можно найти с теоремы Пифагора. OE/2=OK2+KE/2=36+64=100; OE=10 2) радиусы ОА и ОС образуют прямые углы в треугольниках ВАО и ВСО, угол АОВ равен 60 градусов — угол АВО равен 30, катет лежащий напротив угла в 30 градусов, в два раза меньше гипотенузы, BO=2*AO=2*10=20
3) треугольники ЕКО и АКО - прямоугольные с острым углом 60 градусов. Это настолько очевидно, что даже не знаю, как объяснить:))) ну просто угол ЕОК равен половине КОF...
Отсюда немедленно следует ЕО = 2*ОК = 12; АО = (1/2)*ОК = 3; АЕ =9
1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
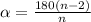
Найдем при каком n угол будет равен 160°:
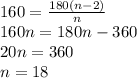
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
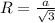
Подставим заданное значение стороны:
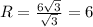
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
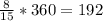 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
сторона основания по пифагору=6v2
высота пирамиды=v(12^2-6^2)=v(144-36)=v108=6v3
объём=1/3*6v3*(6v2)^2=2v3*72=144v3 см.куб.