Доказать: ABCD - прямоугольник.
Доказательство: (картинка ниже)
Т.е. в ABCD стороны попарно равны; все углы прямые, значит, ABCD - прямоугольник.
2)Прямоугольник ABCD, BC делится на 2 отрезка, допустим, BK и KC. Где BK=7,85 a KC=45,6. Т.к.у прямоугольника все углы по 90 градусов, то бисектриса угла А - AK поделит угол А на два ровных угла по 45 градусов, т.е.угол ВАК=KAD=45 градусов. Отсюда, можем найти угол BKA - за Теоремой про сумму углов треугольника, получаем: 180 градусов - (90+45)=45 градусов. Значит треугольник ABK равнобедренный, а т.е. АВ=ВК=7,85см. ВС=7,85+45,6=53,45. Тогда P= 7,85+7,85+53,45+53,45=122,6см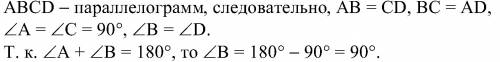
α II β ⇒ ΔABC II ΔA1B1C1 ⇒ AB II A1B1 ; BC II B1C1 ; AC II A1C1
ΔSAB ; ΔSBC ; ΔSAC подобны соответственно ΔSA1B1 ;
ΔSB1C1 ; ΔSA1C1 ⇒
SA : SA1 = SB : SB1 = AB : A1B1 :
SB : SB1 = SC : SC1 = BC : B1C1 ;
SA : SA1 = SC : SC1 = AC : A1C1 ⇒ BC : B1C1 = SA : SA1 ⇔
BC : c = a : (a + b) ⇒
BC =ac/(a + b)