Точка М равноудалена от сторон ромба, следовательно, проецируется в точку пересечения диагоналей ромба.
Расстояние от М до сторон равно длине отрезка МК, проведенного перпендикулярно к стороне ромба. Проекции этого отрезка равна радиусу вписанной в ромб окружности, который, проведенный в точку касания К со стороной ромба перпендикулярен ей.
Диаметр вписанной в ромб окружности равен высоте ромба.
а) Для стороны ромба:
Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Ромб - параллелограмм, все стороны которого равны.
4 АВ²= 16²+12²=256+144=400
АВ²=100 ⇒ АВ=√100=10.
б) Для высоты ромба:
Площадь ромба равна половине произведения его диагоналей.
S=12•16:2=96 см²
Площадь ромба равна произведению высоты на его сторону:
S=h•a; 96=h•10; h=9,6 ⇒ r=9,6:2=4,8 см
Из прямоугольного ∆ МОК искомое расстояние
МО=√(MK²-OK²)=√(64-23,04)=6,4 см
* * *
Формула объема шарового сектора V=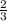
•πR²•h, где h - высота шарового сегмента с той же дугой в осевом сечении шара.
На рисунке приложения это КН.
∆ АОВ - прямоугольный, т.к. дуга АВ=90°
КО=АО•sin45°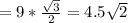
см
KH=R-OK=9-4,5√2=2,636 см²
V=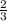•π•81•2,636=142,346π см³
* * *
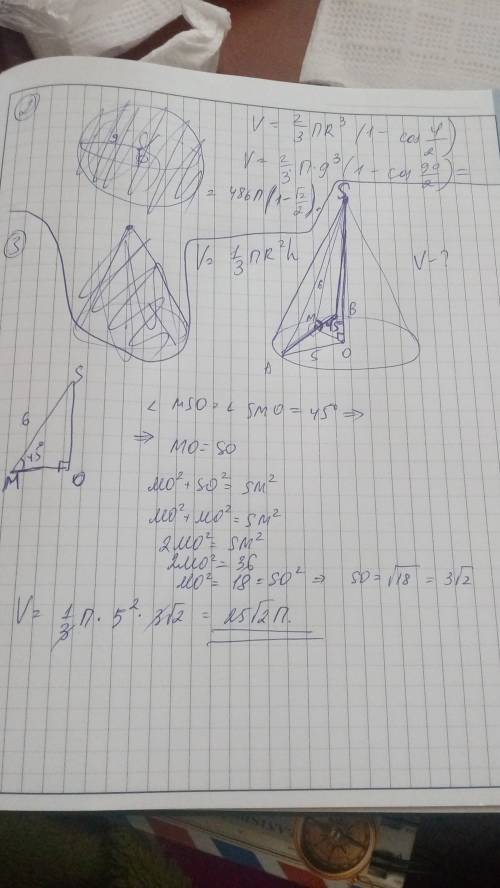
Пусть вершина конуса М, его высота МО, радиус ОА=5 см, хорда АВ - основание сечения, его высота НМ=6 см является расстоянием от хорды до вершины конуса М.
Угол, под которым плоскость пересекает плоскость основания конуса - угол между двумя проведенными перпедикулярно к АВ лучами МН и ОН.
Тогда ∆ МОН - прямоугольный равнобедренный, НО=МО=МН•sin45°
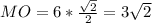
V=S•h=πr²•h
V=π•25•3√2):3=π•25√2 см³
Координаты концов отрезка: A(x₁, y₁) и B(x₂, y₂).
Допустим, что x₂>x₁.
Пусть C - середина отрезка AB с координатами (x, y).
Требуется выразить x и y через координаты точек A и B.
Определение координаты x.
Из точек A, B и C отпустим перпендикуляры на отрезок OX, точки пересечения с осью OX обозначим A₁, B₁ и C₁.
AA₁⊥OX
BB⊥OX
CC⊥OX
Т.к. C - середина отрезка AB, то AC=BC. Т.к. AA₁||BB₁||CC₁, то по теореме Фалеса A₁C₁=B₁C₁.
Значит, C₁ - середина отрезка A₁B₁.
Координаты точки A₁ равны (x₁;0).
Координаты точки B₁ равны (x₂;0).
Координаты точки C₁ равны (x;0).
Длина отрезка A₁C₁ равна x-x₁.
Длина отрезка B₁C₁ равна x₂-x.
Эти длины равны, т.е. x-x₁=x₂-x ⇔ 2x=x₁+x₂ ⇔ x = (x₁+x₂) / 2.
Т.о., координата x середины отрезка есть полусумма координат x концов отрезка.
Определение координаты y.
Выполняется аналогично, выполняя проекцию отрезка AB на координатную ось OY. y = (y₁+y₂) / 2
Т.о., координаты середины отрезка AB есть полусумма соответствующих координат концов отрезка.
C(x;y) = ((x₁+x₂) / 2; (y₁+y₂) / 2)