Дано:
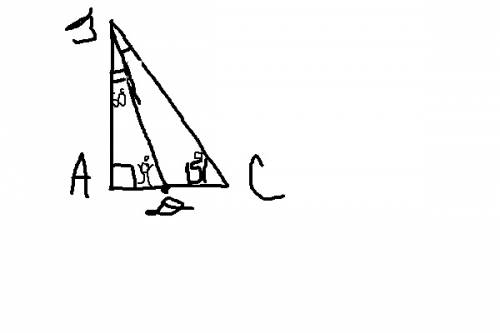
ΔABC,<A=90°
AB=3 см
<C = 15°
<CBD = 15°
Найти:
BD
1)Сумма острых углов прямоугольного треугольника равна 90°. Значит, <B = 90° - 15° = 75°
2)Так как <CBD = 15°, а <ABD = <B - <CBD, то <ABD = 75° - 15° = 60°
3)Рассмотрим ΔABD, <A = 90°. Сумма его острых углов опять же равна 90°. значит, <ADB = 90° - 60° = 30°. AB - катет, лежащий против угла в 30°, BD - гипотенуза. А катет, лежащий против угла в 30°, равен половине его гипотенузы. Значит, BD = 2AB = 3 * 2 = 6 см
Площадь боковой поверхности цилиндра:
Sбок = 2πRH
По условию H = R - 2,
2πR(R - 2) = 160π
R(R - 2) = 80
R² - 2R - 80 = 0 по тоереме Виета:
R = 10 или R = - 8 (не подходит по смыслу задачи)
Н = R - 2 = 8 см
а) Осевое сечение - прямоугольник, стороны которого равны диаметру основания и высоте цилиндра:
Sос. сеч. = 2R · H = 2 · 10 · 8 = 160 см²
б) Сечение цилинра, параллельное оси, имеет форму прямоугольника, одна сторона которого равна высоте. Найдем другую сторону (АВ).
ΔАОВ равнобедренный (АО = ВО как радиусы). Проведем ОС⊥АВ, ОС = 6 см по условию. ОС является так же медианой, ⇒ АС = ВС.
ΔАОС: ∠АСО = 90°, по теореме Пифагора:
АС = √(АО² - ОС²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см
АВ = 2АС = 16 см
Sсеч = AB · H = 16 · 8 = 128 см²
Розглядається прямокутний трикутник SOC. SO - висота