V = 79872√(13) / 1029
r = 32 / 7
R = 80/7
Объяснение:
Площадь боковой поверхности конуса определяется по формуле:
S = π*L*(R + r), где L - длина образующей, R и r - радиусы оснований.
Пусть (х) - коэффициент пропорциональности, обозначим радиус верхнего основания за (2х), радиус нижнего - за (5х).
Подставляем:
128π = π*8*(2х + 5х)
7х = 128π/8π
х = 16/7
Значит: r = 2x = 2 * 16/7 = 32 / 7
R = 5x = 5 * 16/7 = 80/7
Объём усеченного конуса вычисляется по формуле:
V=⅓πH(r²+R*r+R²)
Но для этого необходимо найти высоту усеченного конуса.
Осевое сечение данного усеченного конуса - равнобедренная трапеция.( верхнее основание равно 2r = 2*32/7 = 64/7, а нижнее - 2R = 2* 80/7 = 160/7) В ней малый отрезок, отрезок отсекаемый перпендикуляром (опущенным из вершины верхнего основания на нижнее основание) от большего основания, равен полуразности оснований (по свойству равнобедренной трапеции):
(если обозначить этот отрезок, скажем, за "y")
у = [160/7 - 64/7] / 2 = 96 / 7*2 = 96/14 = 48/7
А высота (из теоремы Пифагора):
Н = √(L² - у²) = √(64 - 2304/49) = √(3136 - 2304) / 7 = √832 / 7 = 8/7 * √(13)
Подставим:
V=⅓*π*H*(r² + R*r + R²) = ⅓*π*8/7 * √(13)*( 1024 + 6400 + 2560) / 49 = 8π/1029 * √(13) * 9984 = 79872√(13) / 1029
Объяснение:
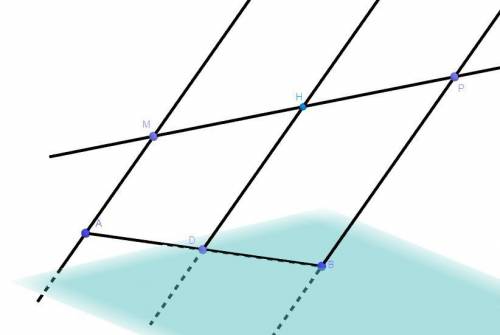
Дано: AM ║DH ║BP, A,B,D ∈ α, D ∈ AB, MH = 12, HP = 8, BD = 14
Найти: AB - ?
Решение: Через прямые AM, DH, BP можно провести одну и ту же плоскость и только одну по теореме, тогда плоскость проведенная через параллельный прямые AM, DH, BP пересекает плоскость по прямой по следствию из аксиом стереометрии. То ест точки A, D, B - лежат на одной прямой и в одной плоскости α (A,B,D ∈ α по условию).Так как по условию AM ║DH и DH ║BP то MADH и BDHP - трапеции по определению, так же эти трапеции лежат на параллельны прямых которые пересекают плоскость α в точках которые лежат на одной прямой тогда по теореме MADH и BDHP - подобные трапеции, следовательно 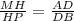 ⇒
⇒ 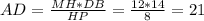 .
.
AB = AD + DB = 14 + 21 = 35.
образующая цилиндра является линией их пересечения.
Сечения цилиндра этими плоскостями являются квадратами и площадь одного из них равна 4 см². Это значит, что высота цилиндра h (его образующая) равна 2см, а поскольку эта образующая является общей стороной квадратов, то квадраты равны.
Проведем через точку А, лежащую на окружности основания цилиндра и являющуюся общей с линией пересечения плоскостей, диаметр АВ. Этот диаметр разделит угол между плоскостями на два равных, поскольку хорды АС и АD (стороны равных квадратов) равны.
Радиус ОЕ, перпендикулярный к хорде АС в точке Н, разделит ее пополам.
Итак, мы получили прямоугольный треугольник АОН с углом ОАН=30° и катетом АН=1см. Тогда по Пифагору АО²-ОН²=АН², где ОА=2*ОН.
Отсюда ОН=√3/3, а ОА=R=2√3/3.
Тогда длина окружности основания равна L=2*πR=2*π2√3/3=4π√3/3.
Площадь боковой поверхности цилиндра будет тогда равна Sб=L*h или Sб=8π√3/3.
ответ: Sб=8π√3/3 ≈14,5 .