2. 42°, 138°
3. 87 и 106 градусов
4. 336, 336, 12, 12
Объяснение:
2. (180° - 96°) : 2 = 42° - меньший угол
42° + 96° = 138° - больший
3. Решим данную задачу при уравнения.
Пусть один из смежных углов х градусов, тогда второй из смежных углов (х + 32) градусов. Нам известно, что сумма градусных мер смежных углов равна 180 градусов. Составляем уравнение:
х + х + 32 = 180;
х + х = 148;
х * (1 + 1) = 148;
х * 2 = 148 (для того, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель);
х = 148 : 2;
х = 74 градусов — один из смежных углов;
74 + 32 = 106 градусов — второй из смежных углов.
4. При пересечении 2 прямых образуется 4 угла, углы ровны попарно
360-(12+12)=336 градуса - это два тупых угла
336:2=168 градуса - один тупой угол
Объем пирамиды равен 54 см³.
Объяснение:
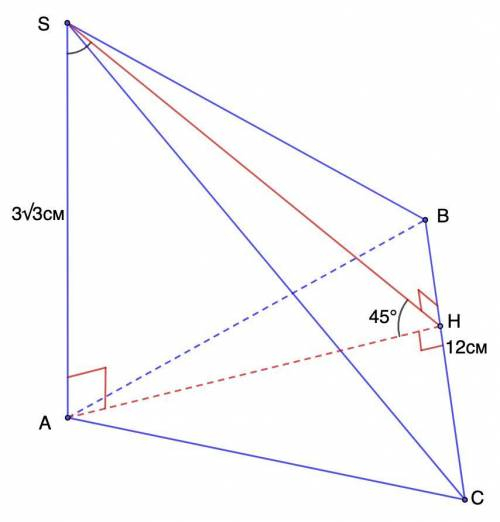
SABC - пирамида. SA перпендикулярен (ABC), SA=3√3 см, BC=12 см, двугранный угол при ребре BC равен 45 градусов . Выполнив рисунок, вычислите объем пирамиды.
Дано: SABC - пирамида;
SA ⊥ АВС;
SA=3√3 см, BC=12 см;
Двугранный угол при ребре BC = 45°.
Найти: V(SABC)
Объем пирамиды найдем по формуле:
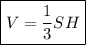 , где S - площадь основания; Н - высота пирамиды.
, где S - площадь основания; Н - высота пирамиды.
Высота пирамиды SA=3√3 см.
Надо найти площадь основания.
1. Рассмотрим ΔASH.
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей этой плоскости.⇒ ΔASH - прямоугольный.
Двугранный угол между двумя плоскостями измеряется линейным углом, образованным двумя лучами, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.АН ⊥ СВ
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.⇒ HS ⊥ CB.
⇒ ∠SHA = 45° - линейный угол двугранного угла SBCA.
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠ASH = 90° - ∠SHA = 90° - 45° = 45°
Если в треугольнике два угла равны, то этот треугольник равнобедренный.⇒ ΔASH - равнобедренный.
AS = AH = 3√3 см.
2. Рассмотрим ΔАВС.
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.ВС = 12 см; AH = 3√3 см.
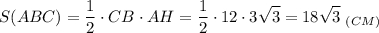
3. Найдем объем пирамиды:
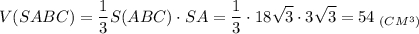
Объем пирамиды равен 54 см³.
#SPJ1
H = √3.
Шестиугольник состоит из 6 равносторонних треугольников со стороной 2.
Площадь одного равна 1/2 * 2 *2* sin60°=1/2 *4 *√3/2 =√3. Значит площадь основания призмы будет 6√3.
V=6√3*√3 = 18.