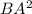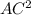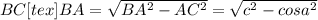= 
+ 
^{2} " alt=" BA = \sqrt{BA^{2} - AC^{2} } = \sqrt{ c^{2} - cosa^{2} }" />^{2} " />
Задача: Треугольник ABC вписан в окружность с центром в точке O. Найти градусную меру угла C треугольника ABC, если угол AOB равен 34°.
Решение: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу:
∠C = ∠AOB/2 = 34/2 = 17°
ответ: ∠C = 17°.
········································································
Задача: AB и AC – отрезки касательных, проведенных к окружности радиуса 8 см. Найти длину OA и AC, если AB = 6 см.
Если к окружности из одной точки (A) проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
AB = AC = 6 см
ΔAOC — прямоугольный, ∠С = 90, т.к. ОС — радиус окружности, а AC — касательная (OC⊥AC по определению)
Величину гипотенузы определим по т. Пифагора:
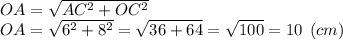
ответ: OA = 10 см, AC = 6 см.
········································································
Задача: На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 26°. Найти ∠NMB.
Вписанный угол измеряется половиной дуги, на которую он опирается (т.к. дуга опирается на соответственный центральный угол):
∠NBA = ∪AN/2 ⇒ ∪AN = 2·∠NBA = 2·26 = 52°
∪BN = 180°−∪AN = 180°−52° = 128°
∠NMB = ∪BN/2 = 128°/2 = 64°
ответ: ∠NMB = 64°.
Боковое ребро правильной треугольной пирамиды образует с плоскостью основания угол 45°. Отрезок, соединяющий середину высоты пирамиды с серединой бокового ребра, равен 3 см. Найдите: а) боковое ребро пирамиды ; б) боковую поверхность пирамиды. - - - - - - -
Дано :
Правильная пирамида PABC ( P -вершина пирамиды ) ; PO ⊥ (ABC) ( О - центр ΔABC ) ;
PM= BM , PN = ON , MN = 3 см ;
∠PAO =∠PBO=∠PCO =45° . PAO =∠PBO=∠PCO - - - - - - - а) PA =PB=PC - ? б) S бок - ?
ответ : а) 6√2 см , б) 27√15 (см³ )
Объяснение: * * * Пирамида правильная , значит ее основание правильный многоугольник (в данном случае равносторонний треугольник) и ее высота проходит через центр основания. * * *
Для удобства обозначаем AB =BC = CA = a . Продолжаем BO , получаем точку H ∈ [AC] и эту точку соединяем с вершиной пирамиды P , PH _ апофема .
ВО = (2/3)*BH =(2/3)*(a√3)/2 = a√3 / 3 || = a / √3 || || ВО = R ( радиус окружности описанной около равностороннего треугольника ABC ) ||
С другой стороны ВО = 2*MN =2*3 см = 6 см (в ΔPOB MN средняя линия → MN =BO/2 , MN || BO ) . Прямоугольный ΔPOB еще и равнобедренный , т.к. по условию задачи ∠PBO= 45° .
PO = ВО ; PB =ВО√2 = 6√2 см || PB = √(PO² + ВО²) || - - -
б) S бок - ?
S бок =3*S(ΔABC) =3*(a*PH /2) = 3a*PH /2 || 3a -периметр основания ||
Апофема PH определим из ΔPOH по теореме Пифагора :
PH =√ (PO²+ОH²) =√ ( ВО² + (ВО/2)² ) = (ВО√5)/2 =(6√5)/2 см =3√5 см.
S бок =3*6√3) *3√5 /2 = 27√15 (см³ )
* * * OH - радиус вписанной в треугольник окружности * * *
* * * PH еще можно определить из определенного ΔPAH * * *
рисунок : см приложение
