Биссектриса AD треугольника ABC равна отрезку DC , AC=2AB. Найдите величину угла ADB в градусах.
Дано: ΔABC ; ∠BAD =∠CAD (AD Биссектриса) ; AD=DC ; AC=2AB - - - - - - - - - - - - - -
∠ADB -?
ответ: 60°
Объяснение: обозначаем ∠C=α ( α _угол острый )
AD = DC ⇒ ∠DAC =∠C=α ; ∠ADB= ∠DAC+∠C = 2α
(∠ADB внешний угол треугольника ADC ) .
∠BAC = 2∠DAC =2α ; ∠B =180° -(∠BAC+∠C) = 180°-3α.
По теореме синусов: AB / sin∠C = AC /sin∠B ⇔
AB / sinα = 2AB/sin (180° - 3α) ⇔ AB / sinα = 2AB / sin3α ⇔
sin3α=2sinα ⇔sinα(3 -4sin²α) =2sinα || sinα≠0 || ⇔ 3 - 4sin²α = 2 ⇔
4sin²α = 1 ⇔ sinα=1/2 α=30° ∠ADB =2α = 60° .
(∠C=30° ; ∠A =60° ; ∠B =90°)
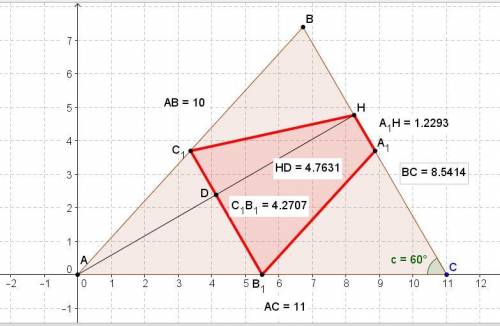
Даны стороны треугольника AB=10, AC=11, и угол ∠C=60°.
По теореме синусов находим угол В.
sin B = 11*sin 60°/10 = 11√3/(10*2) = 11√3/20.
B = arc sin(11√3/20) = 72,29368°.
Находим угол А = 180-60-72,29368 = 47,70632°.
По теореме косинусов находим сторону ВС.
ВС = √(10² + 11² - 2*10*11*cos A) = √(100 + 121 - 220*0,67293) = √72,955189 = 8,541381 .
Находим СН = АС*cos 60° = 11/0,5 = 5,5.
Отрезок ВН = ВC - CH = 8,541381 - 5,5 = 3,041381
Используя косинус угла В = 0,3041381 находим С1Н.
С1Н = √(3,041381 ² + 5² - 2*3,041381 *5*0,3041381) = √25 = 5.
Отрезок НА1 = СН - (ВС/2) = 5,5 - 4,27069 = 1,22931.
Отрезок В1С1 как средняя линя равен (ВС/2) = 4,27069.
Находим А1В1 = √(4,27069 ² + 5,5² - 2*4,27069 *5,5*0,5) = √25 = 5.
Теперь находим диагонали четырёхугольника.
А1С1 = АС/2 = 11/2 = 5,5.
В1Н = √(5,5 ² + 5,5² - 2*5,5 *5,5*0,5) = √30,25 = 5,5.
ответ: сумма периметра и длин диагоналей четырехугольника с вершинами в точках A1, B1, C1 и H равна 2*5 + 1,22931 + 4,27069 + 2*5,5 = 26,5.
По формуле:
Диагонали, соединяющие противоположные вершины: d1=2*a=2*4=8 см
Диагонали, соединяющие вершины, идущие через одну: d2=корень(3)*а=корень(3)*4=1,73*4=6.92