Тангенс угла наклона прямой к оси Ох равен угловому коэффициенту к этой прямой в виде у = кх + в.
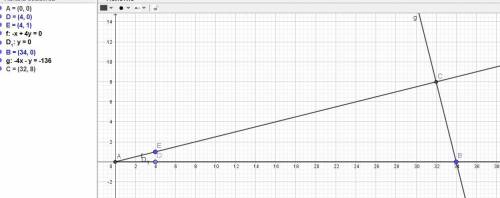
Тогда прямая АС имеет вид у = (1/4)х (в = 0, если точка А в начале координат).
Перпендикулярная прямая ВС имеет к = -1/к(АС) = -1(1/4) = -4.
ВС: у = -4х + в. Подставим координаты точки В(34; 0).
0 = -4*34 + в, отсюда в = 4*34 = 136.
Находим координату х точки Н как абсциссу точки пересечения прямых АС и ВС:
(1/4)х = -4х + 136,
(17/4)х = 136,
х = 136*4/17 = 544/17 = 32.
ответ: АН = 32.
Возможно более простое решение.
Пусть СН = х, АН = 4х.
Угол В = 90 - А.
tg B = ctg А, то есть tg B = 1/(1/4) = 4.
Тогда отрезок ВН = х/4.
Сторона АВ = 34 = 4х + (х/4).
Или (17/4)х = 34, откуда х = 34*4/17.
Так как АН = 4х, то получаем этот же ответ: АН = 4*34*4/17 = 32.
ответ:Для этого прийдется доказать,что треугольник АВD равен треугольнику АСD
Эти треугольники равны по третьему признаку равенства треугольников-по трём сторонам
АВ=СD,по условию задачи
АС=ВD, по условию задачи
АD-общая сторона
Равенство треугольников доказано,а из этого следует,что все соответствующие углы равны между собой
<В=<С
<ВАD=<CDA
<BDA=<CAD
Рассмотрим треугольник АОD
Основание АD
Углы при основании равны между собой(нами это только что было доказано)
<ОАД(он же <САD)=<ODA(он же ВDA)
А если углы при основании равны,то и боковые стороны равны между собой
АО=ОD
И треугольник называется равнобедренный
Объяснение:
H=MO, где O центр основания.
V =(1/3)*S(ABC)*H =(1/3)*a²√3/4*H =(1/3)*6²√3/4*H=3√3*H .
AO =(AB*√3/2)*2/3 =(6*√3/2)*2/3 =2√3.
H= MO =√(MA² - AO²) =√((2√7)² - (2√3)²) =2√(7-3) =4.
Окончательно:
V =3√3*H =3√3*4 =12√3.
ответ :12√3.