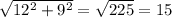
Точки K, E, N , F середины сторон AB,BC,CD и DA выпуклого четырехугольника ABCD. известно что AC=BD=30 см. найдите периметр четырехугольника KENF
Объяснение:
ΔАВС , КЕ-средняя линия , тк по условию точки K, E-середины сторон AB,BC. По т. о средней линии КЕ=1/2*АС=1/2*30=15 (см).
ΔАDС , NF-средняя линия , тк по условию точки N,F-середины сторон CD,DA. По т. о средней линии NF=1/2*АС=1/2*30=15 (см)
ΔАВD , КF-средняя линия , тк по условию точки K, F-середины сторон AB,AD. По т. о средней линии КF=1/2*BD=1/2*30=15 (см)
ΔВСD , EN-средняя линия , тк по условию точки E, N-середины сторон BC,CD. По т. о средней линии ЕN=1/2*BD=1/2*30=15 (см)
P=4*15=60 *см).
a x b = 108 - по правилу площади прямоугольника
a2 + b2 =225 - по теореме Пифагора
Выражаем иЗ первого a= b/108 и подставляем во второе. Имеем биквадратное уравнение 108(2)+ b(4)+108(2)=0
Заменяем переменную. Говорим Пусть х=b(2), получаем обычное квадратное уравнение, решаем через дискриминант, находим корни.
D=50625-46656=3969=63(2)
х=144 и81. Возвращаемся к формуле х=b(2), находим b=12 и 9, отсюда а=9 и 12. ответ стороны равны (9;12) и (12;9)