ответ: Да, это параллелограмм.
Объяснение:
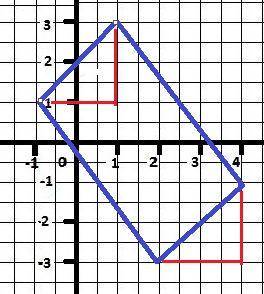
Рисунок задаче в приложении.
Составим уравнения прямых:
ДАНО: А(1;3), В(4;-1) НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(3-(-1))/(1-(4))= - 4/3 = -1,33 - коэффициент наклона прямой
2) b=Аy-k*Аx=3-(- 4/3)*1= 4 1/3- сдвиг по оси ОУ
Уравнение Y(АВ) = - 4/3*x+ 4 1/3
ДАНО: С(2;-3), D(-1;1) НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Сy-Dy)/(Сx-Dx)=(-3-(1))/(2-(-1))= - 4/3 - коэффициент наклона прямой
2) b=Сy-k*Сx=-3-(- 4/3)*2= - 1/3- сдвиг по оси ОУ
Уравнение Y(СD) = - 4/3*x - 1/3
Коэффициент наклона этих двух прямых одинаковый - параллельны.
И длина у них одинаковая - катеты у сторон одинаковый.
ответ:S=12P⋅h,S=12⋅9⋅7√2=97√4
Объяснение:
найдем сторону основания правильной пирамиды по формуле a = R√3, a = √ · √ = 3
найдем периметр основания Р = 3·а, Р = 9
радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. R = 2r, тогда OP=3√2
из прямоугольного треугольника МОР по теореме Пифагора находим апофему МР: MP=MO2+OP2−−−−−−−−−−√,
МР=1+|3√2|2−−−−−−−−√=1+34−−−−−√=7√2
вычислим площадь боковой поверхности правильной пирамиды: S=12P⋅h,S=12⋅9⋅7√2=97√4