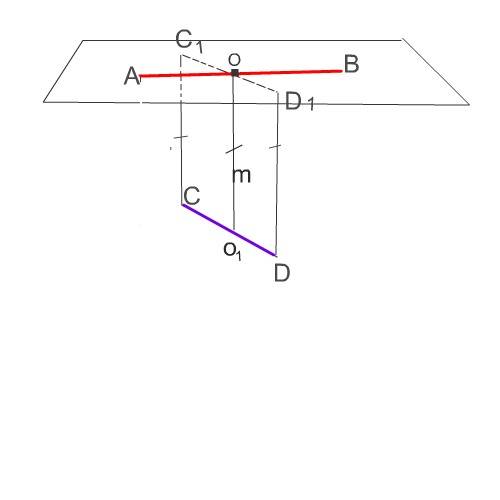
Пусть АВС - данный треугольник. ВК - биссектрисса угла В, пусть Р -произвольная точка на биссектриссе ВК. Опустим перпендикуляры на лучи ВА и ВС. Пусть Е и Т - точки оснований. По определению ЕР и ТР - расстояния от точки Р до сторон ВА и ВС.
Докажем, что ВА=ВС (т.е. требуемое утверждение)
Треугольники РВЕ и РВТ равные, как прямоугольные треугольники с одинаковыми гипотенузами РВ=РВ и равными острыми углами (угол РВЕ=угол РВТ - из определения биссектриссы). Из равенства треугольников следует равенство их сторон
ВА=ВС.
Таким образом
любая точка биссектрисы угла равноудалена от его сторон. Доказано
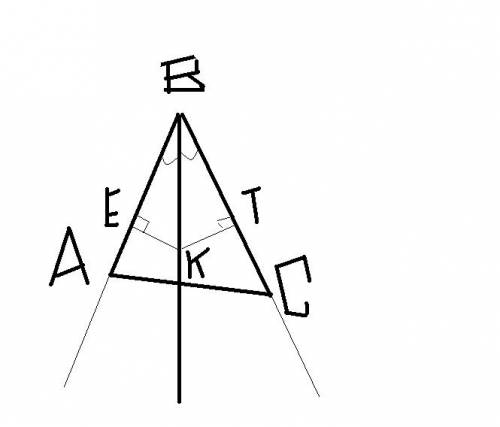
Обозначим скрещивающиеся прямые АВ и СD. Отметим на прямой АВ точку О.
1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Проведем эту плоскость через точку О и прямую СD.
2. Соединим центр СD с точкой О. От концов СD проведем отрезки, параллельные и равные первой прямой. Обозначим их концы С₁ и D₁ соединим.
Мы получили две пересекающиеся прямые АВ и С₁D₁, через которые можно провести плоскость, и притом только одну. Проведенная таким образом плоскость параллельна прямой СD.