ответ:Дан ромб АВСД. диагональ АС пересекает ВД в т.О
АС-меньная диагональ.УголВ=углу Д=60градусов.
Диагонали ромба делят углы пополам=> уголАДО=60:2=30градусов
диагонали ромба перпендикулярны => треугольник АОД прямоугольный.
Катет, лежащий напротив угла 30 градусов равен половине гипотенузы => АО=49:2=24,5
Диагонали ромба точкой пересечения делятся пополам => АС=2*АО=2/24,5=49
Можно и другим
Треугольник АСД - равносторонний, т.к. он равнобедренный (АД=ДС по св-вам ромба), углы при основании равны, а третий угол =60градусов => углы при основании тоже по 60 градусов => АД=АС=49
Объяснение:
ответ: 1 сторона=6см
2сторона=10см
3 сторона 14см
Р=30см
Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
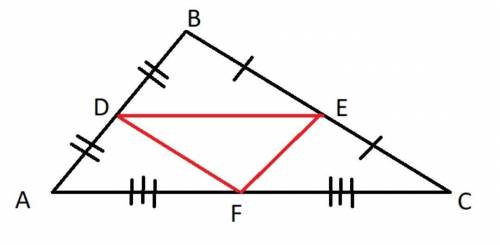
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=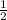
×AB =12÷2=6 см
DF || BC и EF=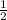×BC=20÷2=10см
DE || AC; DE=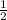×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см
(√8/3)² + cos²А =1
8/9 + cos²А =1
cos²А =1 - 8/9 =9/9 -8/9 =1/9
cos²А =1/9
cos А =√1/9 =1/3
cos А =1/3