Через вершину конуса с основанием радиуса R проведена плоскость, которая пересекает его основание по хорде, которую видно из центра основания под углом α, а из вершины – под углом β. Найти площадь сечения.
--------
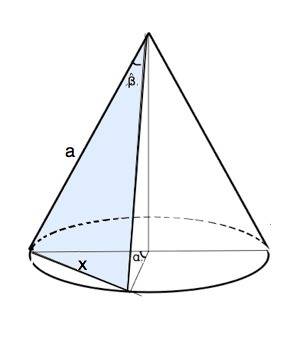
Данное сечение конуса - равнобедренный треугольник. Пусть сторона этого треугольника равна а.
Тогда его площадь можно выразить S=a²•sinβ/2.
1) Примем длину хорды равной х. Тогда из треугольника в основании, образованного хордой и двумя радиусами, квадрат её длины можно выразить по т.косинусов.
х²=2R²-2R²•cosα=2R²(1-cosα)
2) Выразим квадрат длины хорды по т.косинусов из треугольника в сечении:
х²=2а²-2а²•cosβ=2а²(1-cosβ)
3) Приравняем найденные значения х²
2R²(1-cosα)=2а²(1•cosβ)
Выразим а² из этого уравнения:
а²=R²(1-cosα):(1-cosβ)
Отсюда
S сечения=[R²(1-cosα):(1-cosβ)]•sinβ:2
Раз два угла равны между собой, то смотрите:
АDB и BDE углы смежные, т.е. если 180-ADВ сделать.
Так же углы ВEC и ВED смежные, у них так же 180-BEC. Но т.к. между собой эти два угла равны, то получившиеся углы внутри треугольника ВDE тоже будут равны. Треугольник этот получится равнобедренным. А в равнобедренном значит ВD будет равна стороне BE, а значит треугольники
ABD и BEC будут равны по двум сторонам и углу между ними (1 признак равенства). Если треугольники равны - соответствующие элементы равны, т.е. AB = BC. А значит треугольник ABC - равнобедренный)