Гипотенуза с=9√2, один катет а=9, тогда второй катет - в=√((9√2)²-9²)=9. Следовательно треугольник равнобедренный. Углы 90°, 45°, 45°.
Не было под рукой листочка А4, так что нарисовал в paint. Надеюсь, вам будет понятен чертеж.
Итак:
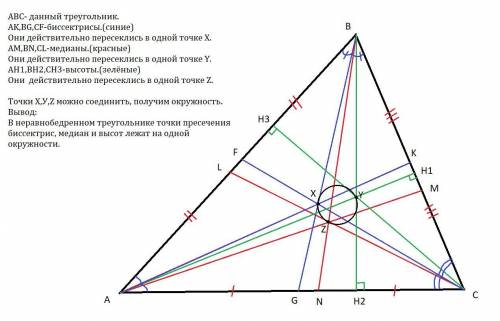
ABC- данный треугольник.(я взял остроугольный, чтобы было удобнее работать с ним)
AK,BG,CF-биссектрисы.(синие)
Они действительно пересеклись в одной точке X.
AM,BN,CL-медианы.(красные)
Они действительно пересеклись в одной точке Y.
AH1,BH2,CH3-высоты.(зелёные)
Они действительно пересеклись в одной точке Z.
Точки Х,У,Z можно соединить, получим окружность.
Вывод:
В неравнобедренном треугольнике точки пресечения биссектрис, медиан и высот лежат на одной окружности.
Ну, собственно, и все.
P.S. А насчет вывода я немного не уверен, просто у меня по счастливой случайности, такой чертеж вышел, а факт этот я не доказывал. Возможно, это и не будет окружностью вовсе, а просто треугольником. Но это решать не мне, а модераторам.
Все рёбра треугольной пирамиды равны. Найти угол наклона:
а) Бокового ребра к плоскости основы.
б) боковой грани к площине основы/
Объяснение:
АВСМ -пирамида, пусть ребро равно х.
a)Угол наклона бокового ребра к плоскости основания это ∠МАО.
Т.к АВ=ВС=АС, то высота проецируется в центр основания О , точку пересечения медиан.Тогда АО=2/3*АН, где АН медиана, ВН=х/2 .
Из ΔАВН-прямоугольного, АН=√(х²-х²/4)=(х√3)/2. Тогда АО=( х√3)/3.
ΔАОМ-прямоугольный, cos∠МАО=АО/АМ , cos∠МАО=( х√3)/3:х=√3/3,
∠МАО=arccos(√3/3) .
ОМ=√(х²-( х√3)/3)² )=(х√6)/3
б)В равностороннем ΔАВС , медиана АН является высотой . Тогда МН⊥ВС по т. о трех перпендикулярах и ∠АНМ-линейный угол между боковой гранью и плоскостью основания.
ОН=1/3*АН , ОН=(х√3)/6.
ΔОНМ-прямоугольный ,tg∠AHM=MO/OH , tg∠AHM=2√2 , ∠AHM=arctg(2√2).

Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
1. b=√ c2−a2 =√(9√2)∧2-9∧2=√81=9
Угол A определится по формуле синуса:
2. sin(A)= a/ c =9/9√2=1/√2
это синус 45°.
Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:
3. B= 180°−90°−A =45°