S осн = 6*а^2*корень из 3/4.
Видим, что надо знать сторону основания :а-?
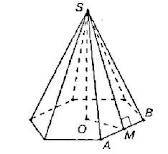
3)S бок = 6*0,5* а*h, где h- апофема .Таким образом, от цели нас отделяет только нахождение стороны основания а. Из тр-ка МОS-прям.: SO = 12, SM =15, тогда ОМ=9 ( либо по теореме Пифагора, либо этот тр-к подобен "египетскому" с коэфф 3).
4)Из тр-ка АОМ-прям: ОМ =9 ,угол ОАМ =60 град., тогда АМ =9/корень из 3 = 3*корень из 3, тогда а = 2*АМ = 6*корень из 3.
5)Sполн = 6* (6*корень из 3)^2 *корень из 3/4+ 3* 6*корень из 3*15 =
= 6*36*3* *корень из 3/4 + 18*15* корень из 3= 6*9*3* *корень из 3 + 18*15* корень из 3 = 18*24* корень из 3 = 432* корень из 3 (кв.ед).
Из треугольника гипотенуза равна 5 см, так как это египетский треугольник.
По свойству точки равноудалённой от вершин треугольника, точка проецируется в центр описанной окружности.
По формуле радиус в прямоугольном треугольнике равен половине гипотенузы.
То есть R=2,5
Из прямоугольного треугольника(катеты это расстояние от точких до плоскости и радиус; а гипотенуза это расстояние от данной точки до вершин треугольника):
Расстояние(х) от точки до плоскости равно:
х"=(6,5)" - (2,5)"=42,25-6,25=36
х=6см
Расстояние от точки до плоскости треугольника равно 6 см.
Так как боковые рёбра наклонены к плоскости основания пирамиды под одним градусом, то основание высоты пирамиды лежит в точке описанной около основания окружности.
Так как треугольник АВС прямоугольный, то центр описанной окружности лежит посередине гипотенузы. АМ=ВМ=СМ.
Пусть АМ=х, тогда АВ=2х.
В тр-ке ЕСМ ЕМ=СМ·tg60=х√3.
Центр шара, описанного около пирамиды, лежит на прямой ЕМ так как только точки этой прямой равноудалены от вершин тр-ка АВС. Поскольку СМ<ЕМ, то центр описанной окружности лежит между точками Е и М. Обозначим его точкой О. АО=ВО=СО=ЕО=6 см.
Пусть МО=у.
В тр-ке СМО СО²=СМ²+МО²=х²+у²=6².
ЕО=ЕМ-МО=х√3-у=6 ⇒ у=х√3-6, подставим это в первое уравнение:
х²+(х√3-6)²=36,
х²+3х²-12х√3+36=36,
4х²-12х√3=0,
4х(х-3√3)=0, х₁=0,
х-3√3=0,
х₂=3√3.
В тр-ке АВС АМ=ВМ=СМ=3√3 см.
ВС=АВ·cos15.
Площадь тр-ка АВС: S=(1/2)АВ·ВС·sin15=(1/2)AB²·sin15·cos15=(AB²·sin30)/4.
S=(6√3)²/8=27/2 см².
Высота пирамиды: Н=ЕМ=х√3=3√3·√3=9 см.
Объём пирамиды:
V=SH/3=27·9/6=40.5 см³ - это ответ.