1), 2), 6), 8).
Объяснение:
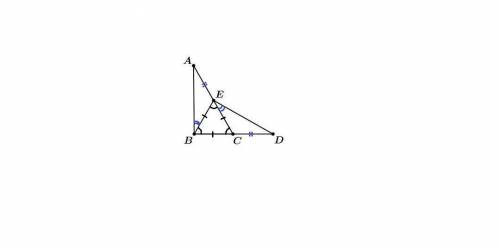
ΔАВС = ΔDEB,
АВ = DE, АС = DB, значит ВС = ВЕ, т.е. ΔВЕС равнобедренный
В равных треугольниках против равных сторон лежат равные углы, значит
∠DBE = ∠ACB, тогда
ΔВЕС равнобедренный с основанием ВС.
Итак, ВЕ = ЕС = ВС, т.е. ΔВЕС равносторонний.
∠АВЕ = ∠АВС - ∠ЕВС
∠DEC = ∠DEB - ∠BEC
∠АВС = ∠DEB из равенства треугольников,
∠EBC = ∠BEC, как углы равностороннего треугольника, значит
∠АВЕ = ∠DEC.
АЕ = АС - ЕС
CD = DB - BC
AC = DB по условию,
ЕС = ВС, так как ΔВЕС равносторонний, значит
АЕ = CD.
1) Треугольник BCE равнобедренный - верно.
2) Треугольник BCE равносторонний - верно.
3) ∠ABC = 90° - нельзя утверждать.
4) Треугольник ECD равнобедренный - нельзя утверждать.
5) AE = BC - нельзя утверждать.
6) AE = CD - верно.
7) ∠ABE = ∠CDE - нельзя утверждать.
8) ∠ABE = ∠CED - верно.


Объяснение:
480 м=0,48 км
200 м=0,2 км.
Имеем прямоугольный треугольник АВС (см. чертеж)
а) по теореме Пифагора АС=√(0,48²+0,2²)=√(0,2304+0,04)=√0,2704=0,52 км
б) по формуле Герона
S=√(p(p-a)(p-b)(p-c))=√(0,6*0,08*0,12*0,4)=√0,002304=0,048 км²
в) ВН⊥АС, т.к. перпендикуляр - кратчайшее расстояние между точкой и прямой, ВН - высота треугольника АВС
S=1/2 * АС * ВН = 0,048, отсюда 0,048=1/2 * 0,52 * ВН
0,26ВН=0,048
ВН=12/65 км.
г) СА=0,52 км; 0,52/5,4=26/270 (часа)≈6 минут