Дано: КМРТ - трапеція, КМ⊥КТ, МТ⊥КР, МО=2 см, ОТ=8 см. Знайти МК.
Трикутники, утворені основами трапеції та відрізками її діагоналей, подібні. Тому ΔМОР подібний ΔКОТ, МО/ОТ=МР/КТ=1/4.
Нехай МР=х см, тоді КТ=4х см.
Якщо прямокутна трапеція має перпендикулярні діагоналі, то довжина висоти трапеції дорівнює середньому геометричному довжин її основ.
МК=√(МР*КТ)=√(4х*х)=√(4х²)=2х см.
Розглянемо ΔКМТ - прямокутний, МР=2+8=10 см.
За теоремою Піфагора МТ²=КМ²+КТ²; 100=4х²+16х²; 20х²=100; х²=5; х=√5
КМ=2√5 см.
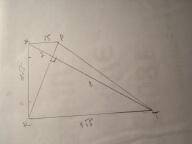
Построим заданную трапецию и проведем диагональ АС
Из условии: ∠ВАС=40°. и ∠САД=25°.
Найдем ∠ВАД:
∠ВАД=ВАС+САД=40+25=65°.
Сумма односторонних углов трапеции равна 180°
Значит ∠АВС=180-ВАД=180-65=115°.
А так как в равнобедренной трапеции углы при основании равны то угол АВС=ВСД и является наибольшим