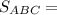4см²
Объяснение:
Смотри прикреплённый рисунок.
О - точка пересечения медиан АМ и BN.
Медианы треугольника точкой пересечения О делятся в отношении 2:1, считая от вершины, поэтому BO =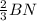 
= 2 см, NO = 
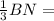1 cм.
Проведём линию MN, соединяющую середины сторон АС и ВС.
MN = 0.5AB, поскольку MN - средняя линия треугольника.
ΔNMC ~ ΔABC по двум углам (∠С - общий, ∠СMN = ∠СBA как соответственные при MN || AB и секущей ВС)
Коэффициент подобия k = MN: AB = 0,5, поэтому площади ΔNMC и ΔABC относятся, как k² = 0.25.
Тогда площадь трапеции ABMN составляет 0,75 площади ΔABC.
Вычислим площадь трапеции ABMN.
.
.
.
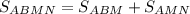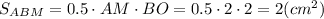
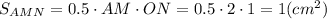
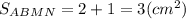
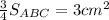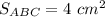1. Найдем отношение ВР к СР;
Через вершину В проводим прямую параллельную АС.
АР продлеваем за точку Р до пересечения с прямой в точке Е.
=> ВЕ параллельно AC;
Треугольники ЕВК и АКМ подобны, следовательно:
ЕВ относится к АМ как ВК относится к КМ;
2) ВК/КМ=1, и ЕВ=АМ; ( треугольники равны).
Отсюда следует: ЕВ = АС/2;
Треугольники ЕВР и АСР подобны
=> ВР/СР = ЕВ/АС = 1/2;
итак СР = ВС*2/3; и, соответственно, площадь треугольника АСР
S ACP= S*2/3; (S - площадь треугольника АВС).
т.к S треугольника ВАМ=1/2 S АВС,
а S АКМ=1/2 S АВМ, то
S AKM = S/4;
Таким образом, площадь четырехугольника КРСМ равна
S KPCM = S ACP - S AKM = S*(2/3 - 1/4) = S*5/12;
ответ 12/5;