Доказательство в объяснении.
Объяснение:
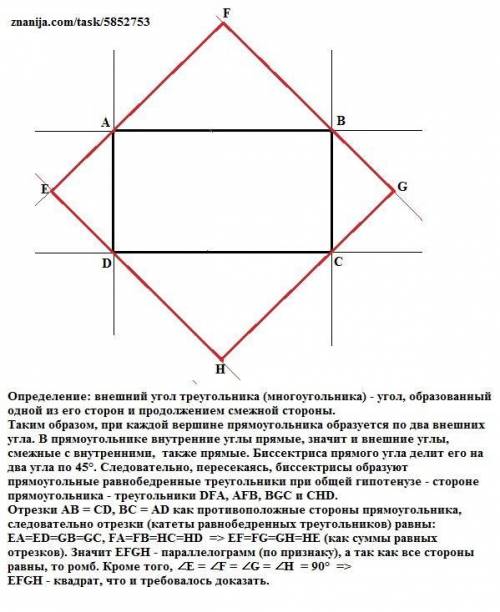
Определение: внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны.
Таким образом, при каждой вершине прямоугольника образуется по два внешних угла. В прямоугольнике внутренние углы прямые, значит и внешние углы, смежные с внутренними, также прямые. Биссектриса прямого угла делит его на два угла по 45°. Следовательно, пересекаясь, биссектрисы образуют прямоугольные равнобедренные треугольники при общей гипотенузе - стороне прямоугольника - треугольники DFA, AFB, BGC и CHD.
Отрезки АВ = CD, BC = AD как противоположные стороны прямоугольника, следовательно отрезки (катеты равнобедренных треугольников) равны: EA=ED=GB=GC, FA=FB=HC=HD => EF=FG=GH=HE (как суммы равных отрезков). Значит EFGH - параллелограмм (по признаку), а так как все стороны равны, то ромб. Кроме того, ∠E = ∠F = ∠G = ∠H = 90° =>
EFGH - квадрат, что и требовалось доказать.
Условие задачи некорректно. Иногда задачи с таким условием составляются специально. Доказательство ниже.
———
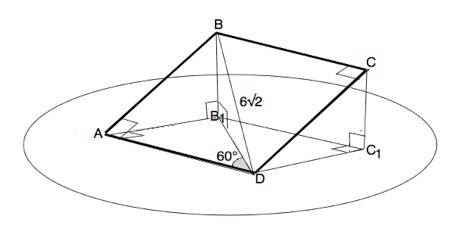
ВВ1 перпендикулярен плоскости альфа, следовательно, этот отрезок перпендикулярен любой прямой, проходящей в этой плоскости через В1.
BD=6√2
∆ ВАD- прямоугольный равнобедренный. Его острые углы равны 45°⇒
AD=BD•sin45°=6
По условию AD лежит в плоскости α.
Поэтому по т. о 3-х перпендикулярах В1А⊥AD, C1D⊥DA, проекция квадрата ABCD на эту плоскость – прямоугольник АВ1С1D.
Угол В1АD- прямой.
Угол В1DА=60°(дано)
Проекция диагонали ВD на плоскость α – гипотенуза В1D
треугольника В1АD
B1D=AD:cos60°=6:1/2=12
———————
Мы получили проекцию наклонной ВD, которая имеет большую длину, чем сама наклонная. Т.е. в прямоугольном ∆ ВВ1D длина катета B1D больше длины гипотенузы BD, чего быть не может. Задача с таким же условием есть от 2015 г, и так именно задумана её составителями.
Но если величина угла В1DА равна 30°,то проекция ВD на плоскост α равна AD:cos30°=4√3.
Или угол В1DB=60° -тоже получится допустимый результат.
если это четырехугольник то L4: 360-180-50=130