Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
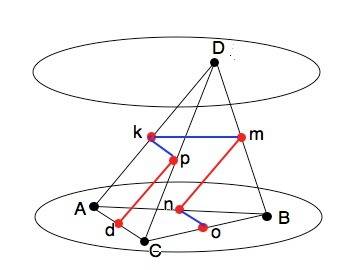
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
Расположим их так, чтобы их вершины совпали. ( см.рисунок в приложении.
Так как по условию стороны этих углов взаимно перпендикулярны,
то КВ⊥АВ, а МВ⊥ВС.
Промежуточные углы КВА и МВС прямые.
Сумма всех четырех углов с общей вершиной равна 360°.
Тогда ∠АВС+∠КВМ=360°-(∠АВК+∠МВС)=180°
Примем коэффициент отношения данных углов равным х.
Тогда 6х+9х=180°, откуда х=12°
Угол АВС=9•12°=108º
Угол КВМ=6•12º=72°