Доказательство в объяснении.
Объяснение:
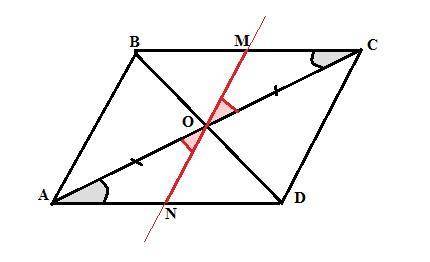
Пусть дан параллелограмм ABCD. AD и ВС - ,большие стороны. Точка пересечения диагоналей, которая делит их пополам, - точка О.
Проведем через точку О прямую, отрезок которой MN лежит между большими сторонами параллелограмма, причем точка M принадлежит стороне ВС, а точка N принадлежит стороне AD.
Тогда треугольники ОМС и ONA равны по двум углам (<MCO=<NAO как накрест лежащие при параллельных ВС и AD и секущей АС, <MOC=<NOA как вертикальные, АО=ОС - половины диагонали АС).
В равных треугольниках против равных углов лежат равные стороны. => OM=ON. Следовательно, отрезок MN делится точкой О пополам, что и требовалось доказать.
найти AB
РЕШЕНИЕ рассмотрим ABO: AO=CO=6 BO=DO=8 (свойство параллелограмма) Из теоремы Пифагора 8^2+6^2= AB^2
AB^2=400
AB=20
ответ: 20