Дан прямоугольник ABCD, ∠CAD:∠CAB=4:5.
Углы прямоугольник равны по 90°.
Пусть ∠CAD=4x, тогда ∠CAB=5x.
∠CAD+∠CAB=∠DAB
4x+5x=9x=90°
x=90°:9=10°
∠CAD=4x=40°
Диагонали в прямоугольнике делятся точкой пересечения пополам.
Пусть AC∩BD=O, тогда AO=DO
В равнобедренном ΔAOD (O-вершина) углы при основании равны. ∠ODA=∠OAD=40°. Сумма углов в треугольнике равна 180°. Откуда ∠AOD=180°-∠ODA-∠OAD=180°-40°-40°=100°
∠AOD>90° ⇒ угол между диагоналями это ∠AOB, смежный с ∠AOD.
∠AOB=180°-∠AOD=180°-100°=80° по свойству смежных углов.
ответ: 80.
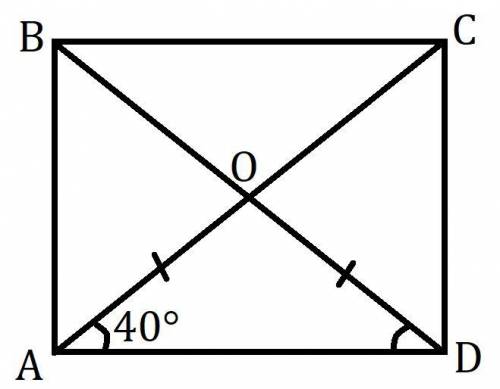
Дан прямоугольник ABCD, ∠CAD:∠CAB=4:5.
Углы прямоугольник равны по 90°.
Пусть ∠CAD=4x, тогда ∠CAB=5x.
∠CAD+∠CAB=∠DAB
4x+5x=9x=90°
x=90°:9=10°
∠CAD=4x=40°
Диагонали в прямоугольнике делятся точкой пересечения пополам.
Пусть AC∩BD=O, тогда AO=DO
В равнобедренном ΔAOD (O-вершина) углы при основании равны. ∠ODA=∠OAD=40°. Сумма углов в треугольнике равна 180°. Откуда ∠AOD=180°-∠ODA-∠OAD=180°-40°-40°=100°
∠AOD>90° ⇒ угол между диагоналями это ∠AOB, смежный с ∠AOD.
∠AOB=180°-∠AOD=180°-100°=80° по свойству смежных углов.
ответ: 80.

1) Дан треугольник со сторонами a=74, b=65√3, c=61.
cos A = (b²+c²-a²)/(2bc) = ((65√3)²+61²-74²)/(2*65√3*61) =
= (12675+3721-5476)/1375,16 = 10920/ 13735.16 =
= 0.79504.
A = 0.651723 радиан = 37.34099°.
cos В = (а²+c²-в²)/(2аc) = ((74)²+61²-(65√3)²)/(2*74*61) =
= ( 5476+ 3721- 12675)/ 9028 = -3478/ 9028 =
= -0.38525.
В = 1.966271 радиан = 112.659°.
cos С = (а²+в²-с²)/(2ав) = ((74)²+(65√3)²-61²)/(2*74*65√3) =
= ( 5476+12675-3721)/16662.33 = 14430/16662.33 =
= 0.866025.
С = 0.523599 радиан = 30°.
2) Не понятно значение стороны c=18/1?