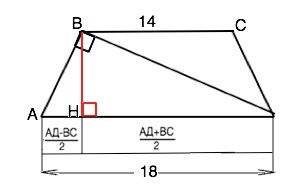
В трапеции АВСD проведем высоту ВН.
Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на отрезки, из которых меньший равен полуразности оснований, больший – их полусумме. (Можно провести вторую высоту из вершины второго тупого угла и получить тот же результат)
АН=(АD-ВС):2=2 см
НD=18-2=16 см
∆ АВD - прямоугольный по условию.
АН –проекция АВ на гипотенузу, HD - проекция BD на гипотенузу.
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Т.е. квадрат высоты равен произведению отрезков, на которые она делит гипотенузу.
ВН²=АН•НD
ВН=√(2•16)=√32
Из прямоугольного ∆ АВН по т.Пифагора
АВ=√(ВН²+АН²)=√(32+4)=6 см
Площадь трапеции равна произведению полусуммы оснований на высоту:
S = (AB + CD)/2 · h
a) h = DH = 0,7 м
S = (2,1 + 1,7)/2 · 0,7 = 3,8/2 · 0,7 = 1,9 ·0,7 = 1,33 м²
б)
АВ = CD - 4 = 13 - 4 = 9 см
S = (AB + CD)/2 · h
h = 2S / (AB + CD)
h = 2 · 77 / (9 + 13) = 2 · 77 / 22 = 7 см