В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.
Трапеция - четырехугольник, и, поскольку в нее вписана окружность, сумма оснований равна сумме ее боковых сторон.
В равнобедренной трапеции высота делит большее основание на два отрезка, из которых больший равен полусумме оснований, а меньший - их полуразности.
Периметр трапеции АВСД равен р
Следовательно,
сумма боковых сторон равна р:2,
сумма оснований равна р:2.
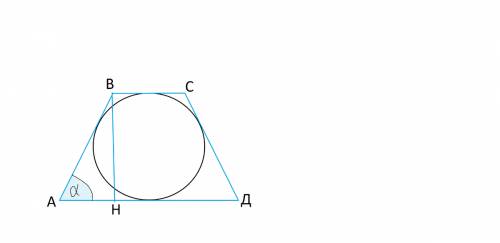
Опустим высоту ВН.
Отрезок НД большего основания равен полусумме оснований и равен (р:2):2=р:4
Боковая сторона АВ равна половине полупериметра трапеции и равна
(р:2):2=р:4
Из прямоугольного треугольника АВН найдем высоту ВН:
ВН=АВ·sin (α)=(р:4)·sin (α)=(р·sin α):4
Площадь трапеции равна произведению высоты на полусумму оснований.
S АВСД=ВН·НД=(р:4)(р·sin (α):4)=(р²·sin α):16 ( единиц площади)
Площадь круга, вписанного в эту трапецию, находим по формуле
S=πr²
Высота трапеции - диаметр этого круга.
Соответственно, его радиус - половина высоты трапеции,
r= ВН:2=(р·sin α):8
а площадь
S= π·{р·sinα }²:64 ( единиц площади).
У этой задачки есть очень наглядное решение.
Можно взять три взаимно перпендикулярные координатные оси и разместить четыре вершины прирамиды в точках (0,0,0) (1,0,0) (0,1,0) (0,0,1). Легко убедиться, что любая из вершин, кроме (0,0,0), является вершиной трехгранного угла, заданного в задаче.
Сама пирамида при этом представляет собой правильную треугольную пирамиду, "боковые" грани которой - равнобедренные прямоугольние треугольники, а "основание" - правильный треугольник с вершинами в точках (1,0,0) (0,1,0) (0,0,1).
Поэтому искомый угол равен 60 градусам.
Эту же мысль (трудно назвать это решением - уж больно просто:)) можно выразить без упоминания координатных осей. Дело в том, что упомянутая пирамида - это часть обыкновенного куба, отсекаемая плоскостью, проходящей через концы трех ребер, имеющих общую вершину.
Берется какая -то вершина куба АBCDA1B1C1D1, например, А, и проводится сечение через точки В, D и А1, у пирамиды А1BDA все трехгранные углы при вершинах "основания" A1BD соответствуют условию задачи. В самом деле, рассмотрим, например, вершину D. Треугольники ADB и ADA1 - равноберенные прямоугольние, поэтому углы АDB и ADA1 равны 45 градусов. Что же касается двугранного угла между плоскостями АDB и ADA1, то это - двугранный угол между гранями куба :), то есть он равен 90 градусам.
Поэтому трехгранный угол при вершине D пирамиды А1BDA удовлетворяет условию задачи. По условию задачи, нужно найти угол A1DB, но он очевидно равен 60 градусам, поскольку треугольник A1DB равносторонний.
∠1 = ∠3 (назовем его так) по признаку вертикальных углов. ∠3 и ∠2 - односторонние, то ∠2 + ∠3 = 180°.
Составим уравнение:
пусть х - ∠2, то х * 2.6 - ∠1.
х + х * 2.6 = 180
3.6х = 180
х = 50
∠2 = 50°.
∠1 = 130°.
Вот:)