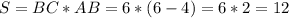 см²
см²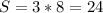
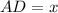 . Тогда
. Тогда 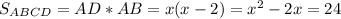
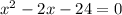 . По теореме Виета находим его корни:
. По теореме Виета находим его корни: 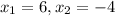 . Так как длина не может быть отрицательной, то выбираем первый корень.
. Так как длина не может быть отрицательной, то выбираем первый корень. 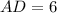 .
. 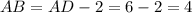 см
см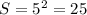 .
.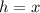 . Тогда наша сторона будет равна
. Тогда наша сторона будет равна  . Учитывая, что площадь треугольника равна
. Учитывая, что площадь треугольника равна 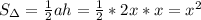 , приравняем это к площади квадрата.
, приравняем это к площади квадрата.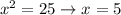
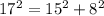 , что делает наш треугольник прямоугольным. Две высоты будут равны соответственно катетам, а третью мы найдем через площадь. Вот как:
, что делает наш треугольник прямоугольным. Две высоты будут равны соответственно катетам, а третью мы найдем через площадь. Вот как: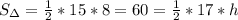
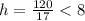 . ответ:
. ответ: 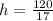
СЕ²=CD²-DE²
DE=AB-AE (а АЕ=ВС, так как трапеция прямоугольная)
DE=17-5=12 см
CE²=15²-12²=81 см
Теперь из треугольника АВС можем найти диагональ АС по теореме Пифагора:
АС²=АВ²+ВС²
AB=СЕ, поэтому можем записать АС²=АВ²+СЕ²
АС²=81+5²=81+25=106
АС=√106