В правильной шестиугольной призме АBCDEFFA₁B₁C₁D₁E₁F₁ все ребра которой равны 1, найдите расстояние от точки В до прямой С₁F
(Правильная призма — это прямая призма, основанием которой является правильный многоугольник.)
-----------
Объяснение подробное и поэтому длинное, хотя решение задачи довольно простое.
Расстояние от точки до прямой - длина отрезка, проведенного от точки перпендикулярно к этой прямой
Соединим попарно точки C₁ и F, B и C₁, B и F.
Если провести через середины ВС и ЕF прямую, то она - диаметр вписанной в основание окружности. ВF параллельна этому диаметру и перпендикулярна СВ.
СВ, проекция наклонной С₁В, перпендикулярна ВF ⇒
по т. о трех перпендикулярах С₁В ⊥BF ⇒
⊿ ВС₁F прямоугольный с прямым углом C₁BF
Искомое расстояние - высота ВН, проведенная из прямого угла этого треугольника к гипотенузе C₁F
C₁F найдем из ∆ С₁BF- он прямоугольный, т.к. все ребра правильной призмы перпендикулярны основанию.
СF равен длине двух сторон основания, т.е. 2.
СС1=1 по условию.
С₁F=√(2²+1²)=√5
C₁B=√(CC₁²+CB²)=√2
BF можно найти по т.косинусов, можно из прямоугольного ∆АВМ, в котором угол АВМ=30º ( как угол при основании равнобедренного ∆ ВАF, где угол при А=120, а угол МАВ=60º).
ВМ =АВ*sin60º=√3):2
BF=2 BM=√3
S ∆ BC₁F=BC₁•BF:2=(√2•√3):2=(√6):2
ВН ∆ BC₁F=2S:C₁F=(√6):√5 или, если извлечь корни, примерно 1,095 (ед. длины)
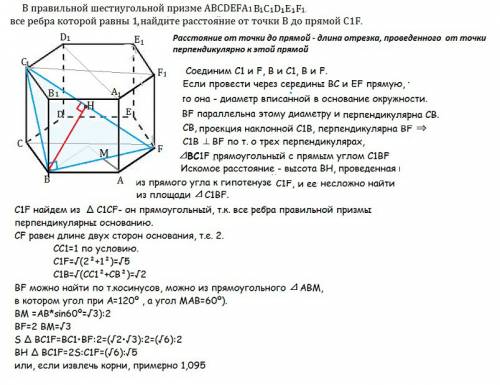
В правильной шестиугольной призме АBCDEFFA₁B₁C₁D₁E₁F₁ все ребра которой равны 1, найдите расстояние от точки В до прямой С₁F
(Правильная призма — это прямая призма, основанием которой является правильный многоугольник.)
-----------
Объяснение подробное и поэтому длинное, хотя решение задачи довольно простое.
Расстояние от точки до прямой - длина отрезка, проведенного от точки перпендикулярно к этой прямой
Соединим попарно точки C₁ и F, B и C₁, B и F.
Если провести через середины ВС и ЕF прямую, то она - диаметр вписанной в основание окружности. ВF параллельна этому диаметру и перпендикулярна СВ.
СВ, проекция наклонной С₁В, перпендикулярна ВF ⇒
по т. о трех перпендикулярах С₁В ⊥BF ⇒
⊿ ВС₁F прямоугольный с прямым углом C₁BF
Искомое расстояние - высота ВН, проведенная из прямого угла этого треугольника к гипотенузе C₁F
C₁F найдем из ∆ С₁BF- он прямоугольный, т.к. все ребра правильной призмы перпендикулярны основанию.
СF равен длине двух сторон основания, т.е. 2.
СС1=1 по условию.
С₁F=√(2²+1²)=√5
C₁B=√(CC₁²+CB²)=√2
BF можно найти по т.косинусов, можно из прямоугольного ∆АВМ, в котором угол АВМ=30º ( как угол при основании равнобедренного ∆ ВАF, где угол при А=120, а угол МАВ=60º).
ВМ =АВ*sin60º=√3):2
BF=2 BM=√3
S ∆ BC₁F=BC₁•BF:2=(√2•√3):2=(√6):2
ВН ∆ BC₁F=2S:C₁F=(√6):√5 или, если извлечь корни, примерно 1,095 (ед. длины)

ОПРЕДЕЛЕНИЕ
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Свойства вертикальных углов
Вертикальные углы равны.
При пересечении двух прямых образуются две пары вертикальных углов и четыре пары смежных углов.