Объяснение:
Первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
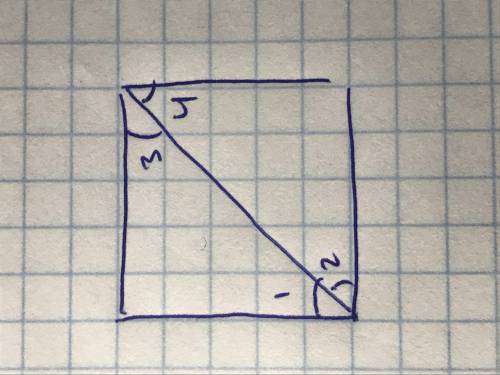
Получается, бисектриса делит квадрат на два треугольника. Треугольники, на которые бисектриса делит квадрат являются прямоугольными, так как углы у квадрата прямые. По определению у квадрата все стороны равны, то есть катеты треугольников тоже будут равны. + углы между сторонами треугольника тоже равны, они 90 градусов. Получается, по первому признаку треугольники, на которые бисектриса делит квадрат равны. А так как треугольники равны, то углы у них тоже равны. Поэтому, угол 1=2, 3=4.
Найдите площадь квадрата описанного вокруг окружности радиуса 28.
Сторона описанного вокруг окружности равна её диаметру.
d = 2R
d = 2 * 28 = 56 (ед.)
Найдем площадь:
S = a²
S = 56 * 56 = 3136 (ед.²)
ответ: 3136 (ед.²)