ответ: 12 (ед. длины)
Объяснение:
Одна из формул биссектрисы треугольника
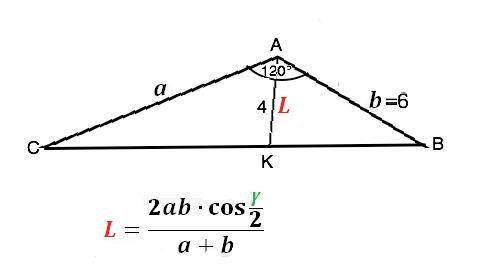
L={2ab•cos(0,5γ)}:(a+b) ,
где L биссектриса, а и b- стороны, γ - угол между ними.
На приведенном рисунке АК - биссектриса ∆ АВС, АС=а, АВ=6, угол А=γ =120°
cos0,5γ=cos60°=1/2
4=2a•6•0,5/(a+6) =>
4a+24=6a =>
АС=a=12 (ед. длины)
Или с тем же результатом найти:
1) По т. косинусов из ∆ АКВ найти КВ
2) по т. синусов из ∆ АКВ угол В
3) из суммы углов треугольника угол С
4) по т. синусов вычислить длину искомой стороны АС
ответ: S=60см²
Объяснение: высота данного треугольника делит его на 2 прямоугольных треугольника, в котором боковая сторона- это гипотенуза, а высота- это катет. По теореме Пифагора найдём 2-й катет получившегося прямоугольного треугольника:
13²-12²=√(169-144)=√25=5см
Мы нашли часть основания первоначального треугольника и, зная, что он равнобедренный, то высота, проведённая к основанию, является ещё и медианой и делит это основание пополам, поэтому часть найденного основания равна второй его части и равна 5см. Поэтому основание треугольника будет: 5×2=10см; основание=10см.
Зная, что площадь треугольника равна полупроизведению его высоты на основание, к которому проведена, найдём площадь треугольника по формуле: ½×а×h, где h-высота, "а"-сторона, к которой проведена высота:
½×10×12=60см²; S=60см²