Нужно найти mm1 при этом , aa1=14 , bb1=4 , am: mb=3: 2. объясните как это сделать

👇

Увидеть ответ

Ответ:

Евгения200605

31.03.2022

ответ: ММ1=8 .

Объяснение:

Нарисуем чертёж, повернув заданный рисунок на 90°.

Продлим стороны АВ и А1В1 до пересечения в точке О . Обозначим ОВ=t.

АМ:МВ=3:2 ⇒ АМ=3х , МВ=2х ( А1М1=3у , М1В1=2у ).

Так как АА1 || BB1 || MM1 , то получим три подобных треугольника: ΔОВВ1≈ΔОММ1≈ΔОАА1 (все по 2-м соответственным углам) . Из подобия следует пропорциональность соответственных сторон:

$\frac{OB}{BB_1}=\frac{OM}{MM_1}=\frac{OA}{AA_1} \; \; \Rightarrow \; \; \frac{t}{4}=\frac{t+2x}{MM_1}=\frac{t+5x}{14}\; \; ; \Rightarrow \\\\14t=4(t+5x)\; \; ,\; \; 14t=4t+20x\; \; ,\; \; 10t=20x\; \; ,\; \; t=2x\\\\\frac{2x}{4}=\frac{2x+2x}{MM_1}\; \; \Rightarrow \; \; \; \frac{2x}{4}=\frac{4x}{MM_1}\; \; ,\; \; MM_1=\frac{4\cdot 4x}{2x}=8$

Нужно найти mm1 при этом , aa1=14 , bb1=4 , am: mb=3: 2. объясните как это сделать

4,4(55 оценок)

Открыть все ответы

Ответ:

Anastasia2003272

31.03.2022

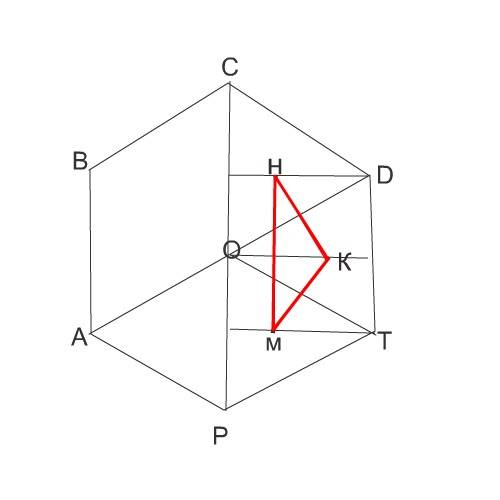
Сделаем рисунок.

СДТР- трапеция.

Площадь ее равна сумме площадей трех равносторонних треугольников.

Отсюда площадь ОСД=27√3:3=9√3

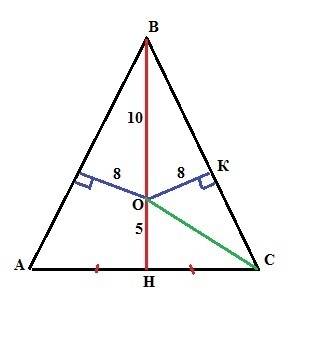
Центр вписанной в треугольник окружности находится на пересечении биссектрис углов. А в равностороннем треугольнике биссектриса одновременно и медиана и высота.

Медианы треугольников пересекаются на расстоянии 2/3 от вершины треугольника, из которой они проведены .

(См. рисунок)

Чтобы найти периметр треугольника, нужно знать длины его сторон.

Сторона МН равна стороне правильного треугольника, из таких треугольниковсостоит данный шестиугольник.

Найдем сторону а из формулы площади правильного треугольника:
S=а²√3):4
Из нее вычислим сторону а
4S=а²√3
а²=4S:√3
а²=4*9√3):√3=36
а=6
НМ=а=6
НК=КМ=1/2 НМ:sin (60)

НК=3:(√3:2)=6:√3=6√3:3=2√3

Периметр Р треугольника МКН - сумма его сторон:
Р=2*2√3+6=4√3+6

Диагонали ср и ад правильного шестиугольника abcдtp пересекаются в точке о. площадь четырёхугольника

4,8(20 оценок)

Ответ:

Бозя1

31.03.2022

Точка О - пересечение медиан, делит каждую медиану в отношении 2:1, считая от вершины (свойство). Значит ВО=10, а ВН=15.
Проведем перпендикуляр ОК - расстояние от точки О до прямой ВС.
Из прямоугольного треугольника ВОК по Пифагору ВК=√(10²-8²)= 6см. КС=ВС-ВК=ВС-6.
Из прямоугольного треугольника КОС по Пифагору ОС²=ОК²+КС².
ОС²= 8²+(ВС-6)² = 64+ВС²-12ВС+36 =ВС²-12ВС+100 (1).
В равнобедренном треугольнике ВН - медиана и высота.
Из прямоугольного треугольника НОС по Пифагору
ОС²=ОН²+НС² = 25+НС².
Из прямоугольного треугольника ВНС по Пифагору НС²=ВС²-15².
Тогда ОС²=25+ВС²-225 = ВС²-200 (2).
Приравняем (1) и (2):
ВС²-12ВС+100=ВС²-200 => 12ВС=300 и ВС=25. АВ=ВС=25см.
НС²=ВС²-15²=НС²=25²-15²=400 и
АС=2*НС = 40см.
ответ: стороны треугольника равны 25,25 и 40.

Расстояния от точки пересечения медиан равнобедренного треугольника до сторон равны 8 см,8 см и 5 см