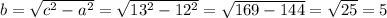
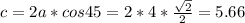Нужна ! : с дан параллелепипед abcdklmn.найдите вектор а=ad+dm+la ,началом и концом котрого служат вершины данного параллепипеда. точка n-середина ребра ac тетраэдра sabc ,m принадлежит bn, вм(век)=2/3bn(век).выразите вектор sm через векторы а=ва,b=bs,с=вс

👇

Ответ:

echo2

04.04.2022

A) Суммой будет вектор, начало которого совпадает с началом первого,
а конец - с концом последнего вектора.
Вектор LA равен вектору MD, значит вектор а=AD, так как сумма векторов DM+MD=0 (сумма противоположных векторов).
ответ: а=AD+DM+LA=AD.
б) Разность двух векторов b и a, имеющих общее начало, представляется направленным отрезком, соединяющим концы этих векторов и имеющим направление «к концу того вектора, из которого вычитают».
Вектор АС равен разности векторов с-а.
Вектор AN=(c-a)/2.Вектор BN=a+(c-a)/2.
Вектор BM=(2/3)*(a+(c-a)/2)=(a+c)/3.
Вектор SM=(a+c)/3 - b = (a+c-3b)/3.
Нужна ! : с дан параллелепипед abcdklmn.найдите вектор а=ad+dm+la ,началом и концом котрого служат в

Нужна ! : с дан параллелепипед abcdklmn.найдите вектор а=ad+dm+la ,началом и концом котрого служат в

4,8(56 оценок)

Открыть все ответы

Ответ:

tanaletinaaaaa

04.04.2022

1) а = 4см, в = 3см;
это треугольник Пифагора. Соотношение его сторон 3:4:5
его гипотенуза равна 5 см. альфа = 30°

2) а = 12см, с = 13см;
третью сторону ищем по теореме Пифагора
$b= \sqrt{c^{2}-a^{2} } = \sqrt{13^{2} -12^{2} } = \sqrt{169-144} = \sqrt{25}=5$

3) альфа = 30°, с = 40см;
это тоже треугольник Пифагора. Гипотенуза с=40см что является 5 частями соотношения.

а=(40/5)*3=24смb=(40/5)*4=32см.

4) альфа = 45°, в = 4см;
при 45° это равнобедренный треугольник.
b=4см.
$c=2a*cos45=2*4* \frac{ \sqrt{2} }{2} =5.66$ см

5) альфа = 60°, в = 5см;
Это тоже треугольник Пифагора.
а=4*(5/3)=20/3 см
с=5*(5/3)=25=3 см

6)с = 10 дм; в = 6дм
треугольник Пифагора
а=(с/5)*4=(10/5)*4=8дм.
альфа = 30°

4,6(80 оценок)

Ответ:

НикаКолядина2000

04.04.2022

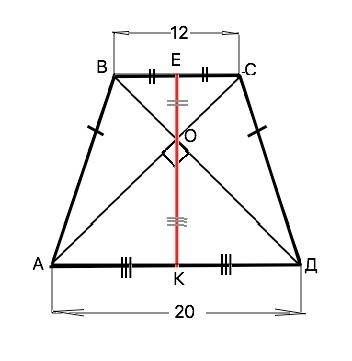
Площадь трапеции равна произведению высоты на полусумму оснований. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований. h=(BC+AD):2 ⇒ h(ABCD)=(12+20):2=16 см. S(ABCD)=h•(12+20):2=16•16=256 см².

Подробнее: В равнобедренной трапеции диагонали равны. Точкой пересечения они делятся пополам и образуют с основаниями равнобедренные прямоугольные треугольники. Высота каждого из них - медиана и равна половине гипотенузы (соответствующего основания трапеции). ОЕ=ВС/2, ОК=AD/2 Высота трапеции h=ЕК=ЕО+ОК. EK=ВС/2+АD:2, т.е.h= (ВС+AD):2 ⇒S=16•16=256 см²