Question

1) в равностороннем △abc на биссектрисе вн взята точка о так, что on⊥bc; om⊥ab (n∈bc, m∈ab). докажите, что △ aom=△noc. найдите углы этих треугольников. 2) в окружности с центром в точке о хорды ав и сd пересекаются в точке n. ∠cnb=150°; cd⊥ob; co⊥ab. найдите ∠cob. 3) в △abc ab=bc, на сторонах ab и аc отмечены точки к и е так, что ке||вс, kh – биссектриса ∠bke; ∠bkh=32°. найдите углы △abc. хотя бы одну !

Answer 1

1) В равностороннем треугольнике высота (к любой стороне) является биссектрисой и медианой; высоты, биссектрисы, медианы (AN, BH, CM) пересекаются в одной точке (O).

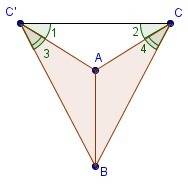
∠OMA=∠ONC=90
∠MAO=∠NCO=∠BAC/2=60/30=30 (в равностороннем треугольнике все углы равны 60, высоты AN и CM являются биссектрисами)
∠AOM=∠NOC=90-30=60 (сумма острых углов прямоугольного треугольника равна 90)
AM=CN=AB/2 (AB=BC, высоты AN и CM являются медианами)
△AOM=△NOC (по стороне и прилежащим углам) 

3) ∠AKE +2∠BKH =180 <=> ∠AKE=180-2*32=116 (∠AKB - развернутый угол, KH – биссектриса ∠BKE)
 ∠AKE=∠ABC=116 (соответственные углы при КЕ||ВС) 
∠ABC+ 2∠BAC =180 (в равнобедренном треугольнике углы при основании равны, сумма углов треугольника 180)
2∠BKH=180-∠AKE=180-∠ABC=2∠BAC
∠BKH=∠BAC=∠ACB=32