Основание треугольника равно 15 см
Объяснение:
Дано:
Смотри прикреплённый рисунок.
ΔАВС - равнобедренный:
АВ = ВС и АС - основание
∠ВАС = ∠АСВ
∠АВС = 0,5 ∠ВАС
АМ - биссектриса
Найти:
Основание АС
Пусть ∠ВАС = ∠ВСА = 2х, тогда ∠АВС = х
Биссектриса АМ делит ∠ВАС пополам, значит
∠ВАМ = 0,5 ∠ВАС = 0,5 · 2х = х.
В Δ АВМ: ∠АВМ = ∠АВС = х.
Δ АВМ - равнобедренный, так как ∠ВАМ = ∠АВМ = х
∠АМС является внешним углом при вершине М для ΔАВМ, поэтому
∠АМС = ∠АВМ + ∠ВАМ = х + х = 2х
Δ АМС - равнобедренный, так как ∠АМС = 2х и ∠АСМ = ∠АСВ = 2х
Тогда АС = АМ = 15 см.
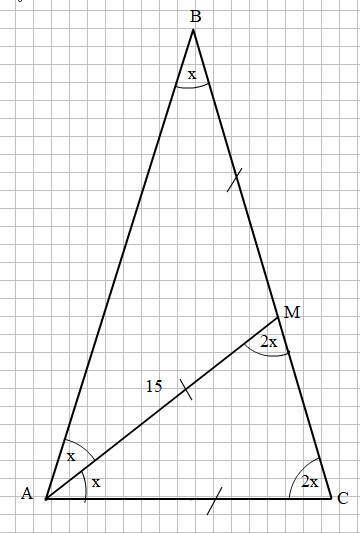
ответ: а) <А=30°, <В=120°, <С=30°; б) АВ=ВС.
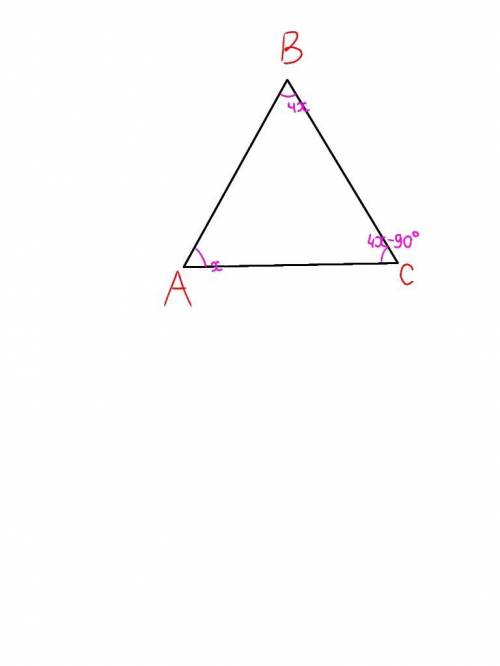
Дано:
∆ ABC
угол А в 4 раза < угла В
угол С на 90° < угла В
<А, <В, <С - ?
а) 1) Пусть угол А - х, тогда угол В - 4х, а угол С = 4х-90°. Составим и решим уравнение:
х+4х+(4х-90) = 180 (по сумме углов треугольника)
х+4х+4х-90 = 180
х+4х+4х = 180+90
9х = 270
х = 270/9
х = 30 → угол А = 30°.
2) Тогда угол В = 4*30° = 120°.
3) Значит, угол С = 120° - 90° = 30°
б) Следовательно, АВ = ВС, тк ∆АВС - равнобедренный - тк <А = <С = 30° (по свой-ву р/б треугольника углы при основании равны).
ответ: а) <А=30°, <В=120°, <С=30°; б) АВ=ВС.
Построим треугольник АВС, площадь которого равна 40 кв. см, Проведем медиану АМ. и обозначим точу Р такую, что АР:РМ=2:3.
Так как медиана треугольника делит его на две равновеликие части, то Sавм=40/2=20 кв. см.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Для наглядности построим высоту ВК – она будет являться высотой как для треугольника ВАМ так и для треугольника ВРМ
Основания Данных треугольников будут соотноситься как 3:5, значит
Sврм : Sвам=3 : 5
Sврм= Sвам*3 / 5=20*3/5=12 кв.см.