Объяснение: ЗАДАНИЕ 1
Площадь шара вычисляется по формуле:
S=4πR², где R- радиус шара=13+6+8=27
S=4π×27²=4π×729=2916(ед²)
Объем шара вычисляется по формуле:
V=4/3πR³=4/3π×27³=4/3π×19683
=26244π(ед³)
ЗАДАНИЕ 2
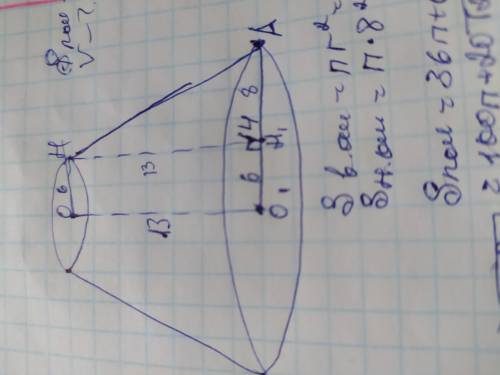
Обозначим радиусы конуса ОН и О1А. Получилась прямоугольная трапеция ОНАО1. Проведём высоту НН1 к радиусу нижнего основания О1А. Она делит О1А так, что О1А=ОН=6, значит Н1А=14-6=8.
Также получился прямоугольный треугольник НАН1, в котором радиусы основания являются катетами а образующая конуса гипотенузой. Найдём НА по теореме Пифагора:
НА²=НН1²+НА²=13²+8²=169+64=233;
НА=√233
Найдём площадь боковой поверхности конуса по формуле:
Sбок=π(R+R1)HA=π(6+14)×√233=20√233π;
√233≈15,3; 20×15,3π=306π
Найдём площадь верхнего и нижнего оснований по формуле: S=πr²
Sверх.осн=π×6²=36π
Sниж.осн=π×14²=196π
Площадь полной поверхности конуса- это сумма всех его площадей основания и боковой поверхности:
Sпол=Sбок.пов+S2хосн=306π+36π+196π==538π
Sпол=538π
Объём усечённого конуса вычисляется по формуле: V=⅓×πH(R1²+R1×R2+R2²)=
=⅓π×13(6²+6×14+14²)=13π/3(36+84+196)=
=13π/3×316=4108π/3(ед³)
или 1369π целых ⅓
ОТВЕТ: Sпол=538π(ед²); V=4108π/3(ед³)
Задание 1.
(Смотри вложение 1 )
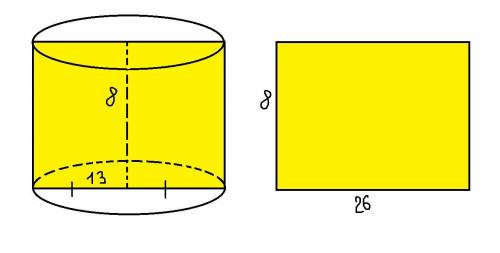
Осевым сечением цилиндра является прямоугольник.
Формула площади прямоугольника: S = a*b , где
а - одна сторона
b - другая сторона
Для нашего прямоугольника высота цилиндра = стороне а, а диаметр ( 2 радиуса) = стороне b. Получается S = 8*26 = 208 см²
Формула площади полной поверхности цилиндра: 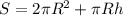 , где
, где
2πR² - площадь оснований
πRh - площадь боковой поверхности
У нас всё известно ⇒ подставляем значения в формулу
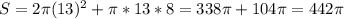 см²
см²
Формула объёма цилиндра: 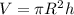 , где
, где
πR² - площадь основания
h - высота
У нас всё известно ⇒ подставляем значения в формулу
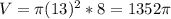 см³
см³
Задание 2.
(Смотри вложение 2 )
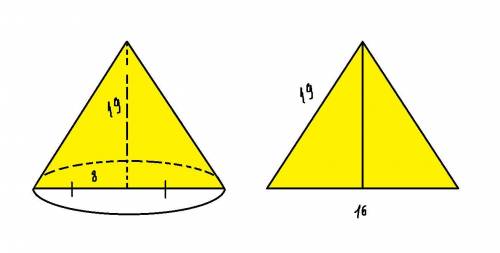
Осевым сечением конуса является треугольник.
Формула площади треугольника: 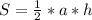 , где
, где
а - основание
h - высота
Для нашего прямоугольника высота конуса = высоте сечения, а диаметр ( 2 радиуса) = основанию . Получается
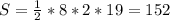 см²
см²
Формула площади полной поверхности конуса: 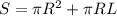 , где
, где
πR² - площадь основания
πRL - площадь боковой поверхности
У нас всё известно ⇒ подставляем значения в формулу
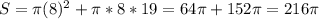 см²
см²
Формула объёма конуса: 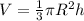 , где
, где
πR² - площадь основания
h - высота
С осевого сечения найдём высоту
По т. Пифагора:
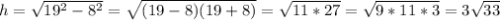
Теперь у нас всё известно ⇒ подставляем значения в формулу
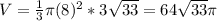 см³
см³