Дано :
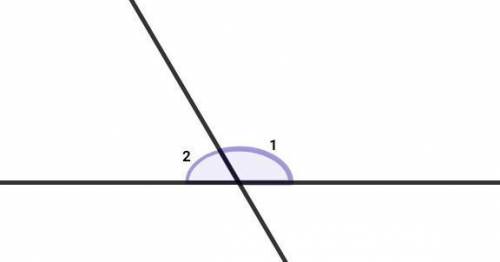
∠1 = 70% от развёрнутого.
Найти :
∠2 = ?
Градусная мера развёрнутого угла равна 180°.70% = 70%/100% = 0,7.
∠1 = 180°*0,7 = 126°.
∠1 и ∠2 — смежные.
Сумма смежных углов равна 180°.Следовательно —
∠1 + ∠2 = 180°
∠2 = 180° - ∠1 = 180° - 126° = 54°.
54°.
Допольнительное построение: высоты, проведенные из точки D на основание АВ- отмечаем точку на основание как Е и из точки С на основание АВ, отмечаем эту точку как F
У нас получился прямоугольник DCFE. DC=FE=10см (потому что стороны DC и FE противолежащие)
AB=AE+EF+FB AE=FB (Треугольник НЕМ= треугольнику LPS по 2 признаку), следовательно FB= (24-10):2=7 см
Расмотрим треугольник ADE, угол DEA=90
Угол ADE=180-(90+60)=30
AE=1/2 AD( напротив угла 30 градусов), следовательно AD=AE*2 AD=7*2=14см
AD=CB=14см( ABCD равнобедренный)
P=DC+CB+AB+AD P=14+14+24+10=62см
ответ: периметр трапеции 62 см.
Объяснение:
а || b
c - секущая.
АМ - биссектриса ∠DAK
DB - биссектриса ∠ADM
Доказать:АМ ⊥ DB
Решение:При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 180°.
Возьмём любые градусные меры углов DAK и ADM, но при условии, что их сумма будет равна 180°.
Допустим ∠DAK = 100˚, тогда ∠ADM = 80˚
Так как АМ и DB - биссектрисы => ∠1 = ∠2 = 100°/2 = 50° и ∠3 = ∠4 = 80°/2 = 40°
В прямоугольном треугольнике сумма острых углов равна 90°
40° + 50° = 90° => △ADB - прямоугольный.
=> DB ⊥ AM
Вывод: мы можем взять любые градусные меры ∠DAK и ∠ADM, но при условии, что сумма их будет равна 180°.
Ч.Т.Д.
54°
Объяснение:
ПОЛНОЕ УСЛОВИЕ В ПРИЛОЖЕНИИ
∠1+∠2=180° - т.к они смежные
70%=70:100=0,7
∠1=180°×0,7=126°
∠2=180°-126°=54°
∠1+∠2=180° - т.к они смежные
100%-70%=30%
∠2=180°*0,3=54°