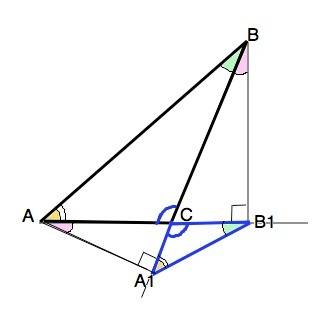
Высоты тупоугольного треугольника, проведенные из вершин острых углов, пересекают прямые, содержащие их стороны, вне треугольника.
Рассмотрим прямоугольные ∆ АСА1 и ∆ ВСВ1.
Острые углы при С у них равны как вертикальные.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны. ⇒
∆ АСА1 ~ ∆ ВСВ1
Тогда синусы их равных углов равны, т.е. отношение сходственных катетов к гипотенузам, равно. СА1/ АС=СВ1/ВС
III признак подобия треугольников.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Доказано.
Величина угла между плоскостями – угол, сторонами которого являются лучи, по которым эти плоскости пересекаются плоскостью, перпендикулярной ребру угла.
Искомый угол –это угол DHC, образованный отрезками СН и DH (см. рисунок в приложении).
СН - высота ∆ АВС, DC –⊥ плоскости ∆ АВС по условию, DH ⊥ АВ по т. о трёх перпендикулярах,
плоскость DHC перпендикулярна АВ.
СН как катет ∆ АНС, противолежащий углу 30º, равен половине гипотенузы АС и равен а/2
Тангенс угла DHC=DC/HC=[(а√3):2]:a/2=√3.
Это тангенс угла, равного 60º.
Угол между плоскостью (ADB) и плоскостью (ACB)=60º.