Отрезки АВ и CD пересекаются в точке O так, что ∠ACO = ∠BDO, AO:OB = 2:3. Найдите периметр треугольника АСО, если периметр треугольника ВОД равен 21 см.
============================================================
∠ACO = ∠BDO - как накрест лежащие углы ⇒ АС || BDΔACO подобен ΔBOD по двум углам (∠АСО = ∠BDO - по условию, ∠BOD = ∠AOC - как вертикальные углы)" Периметры подобных треугольников относятся как коэффициент их подобия "Р bod / P aco = 3 / 2P aco = 2 • P bod / 3 = 2 • 21 / 3 = 2 • 7 = 14 смОТВЕТ: 14 см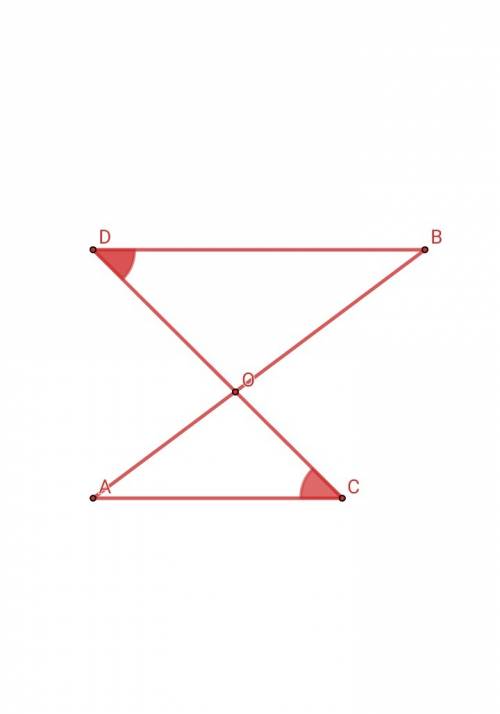
am=cm=a1m1=c1m1.
Рассмотрим треугольники abm и a1b1m1. Они равны по трем сторонам:
- ab=a1b1 по условию;
- bm=b1m1 по условию;
- am=a1m1 как только что доказано.
У равных треугольников abm и a1b1m1 равны соответственные углы amb и a1m1b1. Значит, углы bmc и b1m1c1, равные 180-<amb и 180-<a1m1b1, также равны между собой.
Треугольники bmc и b1m1c1 будут равны по двум сторонам и углу между ними:
- bm=b1m1 по условию;
- сm=c1m1 как было показано выше;
- углы bmc и b1m1c1 равны как доказано выше.
У равных треугольников bmc и b1m1c1 равны соответственные стороны bc и b1c1.
Таким образом, треугольники abc и a1b1c1 получаются равными по трем сторонам.