Путься трапеция прямоугольная и угол DAB прямой. Тогда двумя меньшими сторонами являются стороны AB и BC и они равны по 6 см, опустим перпендикуляр из С к стороне AD. у нас получится квадрат ABCD. У квадрата все углы равны 90 градусов. По условию известно, что больший угол равен 135, большим углом является угол BCD, следовательно угол OCD равен 135-90=45. угол CDO равен 180-90-45=45. у треугольника COD два угла равны, следовательно, он является равнобедренным и сторона CO=OD=6см. Теперь вернемся к нашей трапеции, AO+OD=12 см
Площадь трапеции равна произведения полусуммы оснований на высоту. Тоесть (6+12)/2*6=54см^2
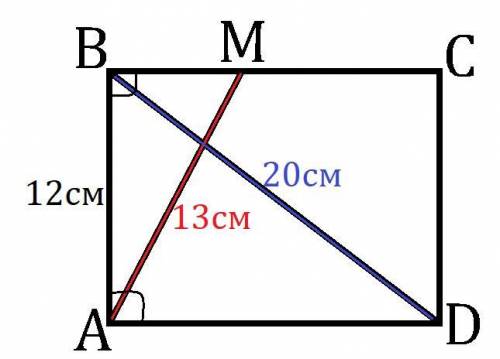
В прямоугольном ΔBAD (∠A=90°):
AB=4·3см, BD=4·5см значит, по Египетскому треугольнику AD=4·4см=16см.
AD = BC = 16см, как противоположные стороны прямоугольника ABCD.
В прямоугольном ΔABM (∠B=90°):
AB=12см, AM=13см значит, по Пифагоровой тройке BM=5см;
Ну или по теореме Пифагора BM = √(AM²-AB²) = √(13²-12²) = √((13-12)(13+12)) = √25 = 5 см.
MC = BC-BM = 16-5 = 11 см
S(AMCD) = S(ABCD) - S(ABM) = AB·AD - 
AB·BM = 12·16-12·5:2 = 6·(32-5) = 6·27 = 162 см²
ответ: MC=11см и S(AMCD)=162см².
Можно было найти S(AMCD), как площадь трапеции, основания которой MC=11см, AD=16см и высота CD=AB=12см. Тогда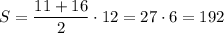 
см².
cos^2 = 1 - sin^2 = 1 - (12/13)^2 =25/169
cos = 5/13
2)найти тангенс острого угла, если его синус равен 12\13
cos = 5/13
tg = sin/cos = 12/13 / 5/13 = 12/5