Объяснение:
12
Если диагональ образует с площадью основания,то диагональ основания равна высоте прямоугольного параллелепипеда.
Найдём диагональ основания по теореме Пифагора:
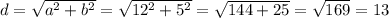
h=d=13 см
S = 2(a · b + a · h + b · h)=2(12 · 5 + 12 · 13 + 5 · 13) =2(60+156+65) = =2*281=562 см²
V=a · b · h=12 · 5 · 13=780 см³
13
Если образующая конуса наклонена к плоскости основания на 45°,то радиус основания равен высоте.Примем радиус основания за х,тогда по теореме Пифагора:
l²=2r²
12²=2x²
x²=144:2
x²=72
x=√72=6√2 см
S=π r (r + l)=π6√2(6√2+12)=π72+π72√2=π72(1+√2) см²
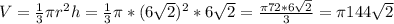
V=144√2 π см³
На сторонах треугольника АВС АВ, ВС, СА взяты соответственно точки М, N, P таким образом. что выполняется соотношение АМ:АВ=ВN:NB=СР:СА=1:3. Найдите площадь треугольника АВС, если площадь треугольника МNP=2.
———————
ответ D) 6
Объяснение: Пусть АВ=с, ВС=а, АС=b
Т.к. короткие части равны 1/3 каждой стороны, то АМ=с/3, ВN=a/3, CP=b/3. Соответственно вторые части сторон равны по 2/3 от длины каждой.
Одна из формул площади треугольника S=0,5•a•b•sinα, где а и b - стороны. α - угол между ними. Следствие из этой формулы:
Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Примем площадь ∆ АВС=Q.
Тогда Ѕ(МАР):Ѕ(АВС)=[(с/3)•2b/3]:c•b=Q•2/9
Аналогично вычисления площадей ∆ МВN и ∆ PNC дадут их величину Q•2/9 (проверьте)
Сумма площадей этих треугольников 3•Q•2/9=Q•2/3 =>
Q-2Q/3=2
Q/3=2 => Q=3•2=6 (ед. площади)