Два треугольника равны по третьему признаку равенства треугольников, если ...
Выберите один из 3 вариантов ответа:
1) две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника ;
2) сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника ;
3) три стороны одного треугольника соответственно равны трём сторонам другого треугольника.
ответ: 3).Задание №2.Дано:ΔABD и ΔCBD;
AB = BC;
AD = DC.
Доказать:ΔABD = ΔCBD
Доказательство:1. AB = BC (по условию) |
2. AD = DC (по условию |⇒ ΔABD = ΔCBD (по третьему признаку).
3. BD - общая сторона |
Что и требовалось доказать!
ответ: 2).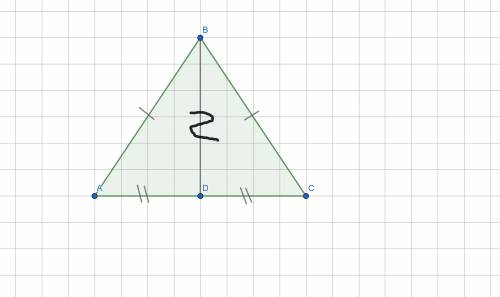
По условию ∠АВС=2∠А, значит, ∠АВД=∠А, следовательно и ВД=АД=6 см.
По свойству биссектрисы треугольника
АД\ДС = АВ\ВС
АВ\ВС=2; АВ=2ВС.
Пусть ВС=х, тогда АВ=2х
По свойству биссектрисы треугольника
ВД²=АВ*ВС-АД*ДС
6²=2х*х-6*3
36=2х²-18
2х²=54
х²=27
х=3√3
ВС=3√3 см; АВ=2*3√3=6√3 см; АС=9 см.
(Сделал точный чертеж к задаче для полной наглядности)