Задание 2
Дано:
DO = OC
AO = OB
Доказать, что треугольник CAO равен треугольнику DBO
Доказательство
Рассмотрим треугольник CAO и треугольник DBO
DO = OC - по условию
AO = OB - по условию
угол DOB равен углу AOC, т.к. углы вертикальны
следовательно треугольник CAO равен треугольнику DBO по 1 признаку равенства треугольников
ч.т.д
Задание 4
Дано:
AD- биссектриса
угол ADB = углу ADC
Доказать, что AB = AC
Доказательство
Рассмотрим треугольник ABD и треугольник ACD
угол ABD = углу ADC - по условию
угол BAD = углу DAC - т.к AD - биссектриса
AD - общая
следовательно треугольник ABD = треугольнику ACD по 2 признаку равенства треугольников
следовательно AB = AC
ч.т.д
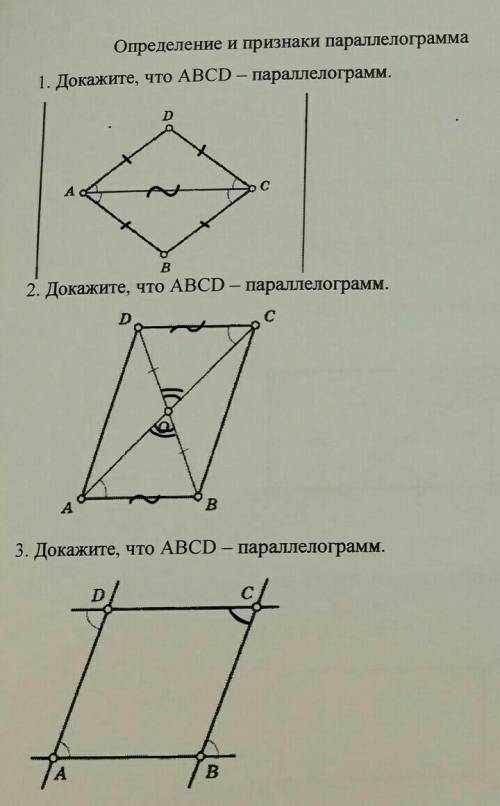
1) Дано: ∠DAC = ∠DCA = ∠CAB = ∠BAC.
Доказать: ABCD - параллелограмм.
Доказательство: Рассмотрим ΔABC и ΔAD.AC - общая сторона, ∠DAC = ∠DCA = ∠CAB = ∠BAC (по условию) ⇒ ΔABC = ΔAD по стороне и двум прилежащим к ней углам.Так как треугольники равны, то и их соответствующие элементы равны. ⇒ AD = BC ; AB = DC. ⇒ABCD - параллелограмм, так как в этом четырёхугольнике противоположные стороны попарно равны.
ответ: что и требовалось доказать.
2) Дано: DO = OB ; ∠OAB = ∠DCO.
Доказать: ABCD - параллелограмм.
Доказательство: Рассмотрим прямые DC и AB при секущей AC.Накрест лежащие углы ∠OAB = ∠DCO (по условию) ⇒ DC║AB.
Рассмотрим ΔAOB и ΔDOC.∠OAB = ∠DCO (по условию) ; DO = OB ; ∠AOB = ∠DOC (вертикальные). ⇒ ΔAOB = ΔDOC по стороне и двум прилежащим к ней углам.Так как треугольники равны, то и их соответствующие элементы равны. ⇒ AB = DC. ⇒ ABCD - параллелограмм, так как в этом четырёхугольнике две противоположные стороны параллельны и равны.
ответ: что и требовалось доказать.
3) Дано: ∠D = ∠A = ∠B.
Доказать: ABCD - параллелограмм.
Доказательство: Рассмотрим прямые DC и AB при секущей AD.Накрест лежащие углы ∠D = ∠A (по условию) ⇒DC║AB.Так как DC║AB, то ∠B = ∠C (как накрест лежащие углы при пересечении параллельных прямых секущей).Теперь рассмотрим прямые AD и BC при секущей DC.Соответственные углы ∠D = ∠C (по выше доказанному) ⇒ AD║BC. ⇒ ABCD - параллелограмм, так как в этом четырёхугольнике противоположные стороны попарно параллельны (по определению).
ответ: что и требовалось доказать.
лежат на этой высоте к основанию...
площадь треугольника можно вычислить по формуле Герона (т.к. известны три стороны),
из площади найти ту самую высоту-биссектрису-медиану))
и еще две формулы площади найти радиусы...