Задача 1.
Попытаюсь объяснить подробней)
СА и СВ - это отрезки касательных, проведённых из одной точки.
ОА и ВО - это радиусы, проведённые в точки касания прямых с окружностью. По св-ву этих особых радиусов мы знаем, что они перпендикулярны касательным. Т.е. углы САО и СВО = 90°.
Треугольник АВО р/б, т.к. АО и ВО - радиусы. Если один из углов при основании = 40, то и второй = 40. По сумме углов треугольника: 180-(40+40)=100° - угол АОВ.
САОВ - это четырёхугольник, в котором все углы в сумме дают 360°.
∠АСВ - это угол между касательными. Его можно найти, если вычесть из 360° сумму всех остальных трёх углов четырёхугольника.
∠АСВ = 360°-(90°*2+100°)=80°.
ответ: 80°.
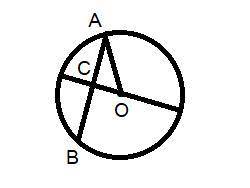
Задача 2. (рисунок №1 во вложении).
Сразу скажу о свойстве диаметра (в нашем случае это радиус, но значения не имеет): диаметр, перпендикулярный хорде, делит эту хорду пополам. Значит, СА = ВА = 20:2 = 10см.
Треугольник АСО прямоугольный, т.к. ∠АСО = 90°. Если один из острых углов прямоугольного треугольника = 45°, то и второй угол = 45°. Отсюда, ΔСАО равнобедренный, СА=СО=10см.
ответ: 10см.
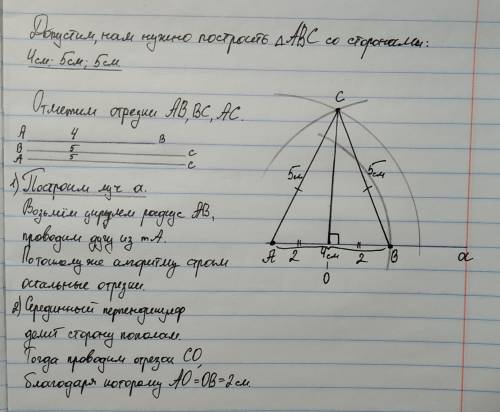
Задача 3. (рисунок №2 во вложении).
Построение треугольника во вложении, а инструкция построения серединного перпендикуляра здесь:
ВС – отрезок, к которому требуется построить серединный перпендикуляр. Построим две окружности радиуса ВС с центрами С и B. Они пересекутся в двух точках – доустим, К и L. Проведем прямую КL. Она является серединным перпендикуляром к отрезку ВС.
Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
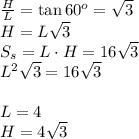
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
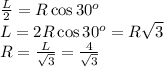
Запишем теперь выражение для площади боковой поверхности цилиндра:
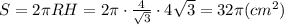
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
∠A = 64°
∠B = 50°
AD и ВE - биссектрисы ∠A и ∠B
О ∈ AD, O ∈ BE
Найти:
∠АОВ
Решение
За условием АD и ВЕ - биссектрисы ∠А и ∠В. Найдем ∠ОАВ и ∠АВО:
∠ОАВ = 64° : 2 = 32°; ∠ОВА = 50° : 2 = 25°. За теоремой про сумму углов треугольника ∠ОАВ + ∠АВО + ∠АОВ = 180°. Найдем ∠АОВ:
∠АОВ = 180° - (32° + 25°) = 123°.
ответ: 123°