ответ: 6 (ед. площади)
Объяснение решения задач на площадь трапеции, в которой известны основания и диагонали, обычно сводится к проведению прямой из вершины при одном основании параллельно диагонали до пересечения с продолжением другого основания и затем вычислением площади получившегося треугольника. .
Подробное решение.
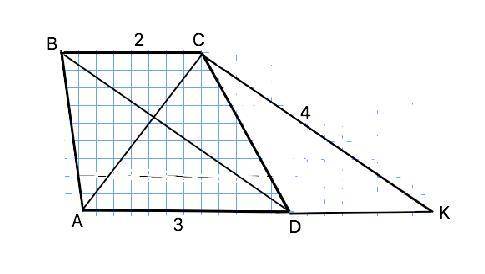
Пусть в трапеции АВСD BC||АD, AD=AC=3, ВС=2, BD=4.
Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=h•(BC+AD):2
Проведем СК||ВD. Тогда ВС||DC, CK|| BD => BCKD - параллелограмм, и DK=BC=2 =>
AK=AD+DK=3+2=5.
Ѕ(∆ АСК)=h•AK:2=S(ABCD)
Вычислив площадь треугольника АСК по т.Герона получим S(ABCD)=S(ACK)=6.
Но конкретно для этой задачи с отношением сторон треугольника АС:СК:АК=3:4:5 проще вычислить площадь треугольника АСК как произведение диагоналей трапеции – этот треугольник прямоугольный ( египетский).
S(ABCD)=S(ACK)= АС•СК:2=3•4:2=6 (ед. площади).
Проведем в окружности два диаметра: один параллельно хорде, другой - в точку касания.
ОК, проведенный в точку касания, перпендикулярен касательной, значит, перпендикулярен и хорде, т.к. она параллельна касательной (свойство).
По свойству радиуса, перпендикулярного хорде, он делит хорду пополам.
Соединив центр окружности и конец В хорды, получим прямоугольный ∆ ОМВ с гипотенузой ОВ= r=65 см, катетом МВ=126:2 =63 см ( половина хорды) и катетом ОМ, являющимся расстоянием от диаметра до хорды.
.По т.Пифагора
ОМ=√(ОВ²-МВ²)= √256=16 (см)
Расстояние от точки до прямой - это длина перпендикуляра, проведенного от точки к этой прямой.
МК - перпендикулярен касательной и является искомым расстоянием.
Тогда это расстояние будет:
МК=ОК-ОМ=65-16=49 (см) - если хорда расположена между диаметром и касательной,
и
МК1=r+ОМ=65+16=81 ( см)- если между хордой и касательной расположен диаметр.
ответ: 49 см или 81 см

С1С2=4 по условию
СС1-высота равностороннего треугольника,
СС2-по т. Пифагора
CC1^2=(2√3)^2-(√3)^2=12-3=9; CC1=3
CC2^2=4^2+3^2=25
CC2=5