ответ: 6 целых 4/7
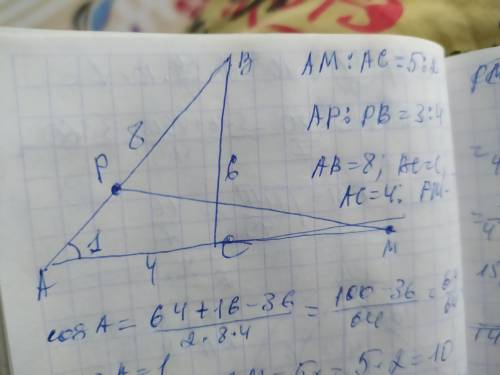
Объяснение: рассмотрим ∆АВС. В нём известны 3 стороны, и мы можем найти используя теорему косинусов угол А:
cosA=(AB²+AC²-BC²)/2×AB×AC=
=(8²+4²-6²)/2×8×4=(64+16-36)/64=64/64=1
cosA=1
Обозначим пропорции для разных сторон как: АМ=2х, 5х, а АВ как 3у, 4у
АМ=5х; АР=3х; ВР=4х
АС=4=2х.
2х=4
х=4÷2=2; х=2
АМ=5×2=10; АМ=10
Составим уравнение по стороне АВ:
3у+4у=8
7у=8
у=8/7
АР=3у=3×8/7=24/7;. АР=24/7
Найдём РМ, используя теорему косинусов: РМ²=АР²+АМ²-2×АР×АМ×cosA=
=(24/7)²+10²-2×24/7×1=
(576/49)+100-(480/7)= здесь находим общий знаменатель и получаем:
(576/49)+(4900/49)-(3360/49)=
=2116/49; РМ=√2116/49=46/7
или 6 целых 4/7
V2- объем конуса ПОСЛЕ изменений
1. h=H/2 r=2R
V2=πr²h/3
V2=4πR²H/6=2πR²H/3- объем конуса после изменений
V1/V2=πR²H/3 : 2πR²H/3
V1/V2=1/2
V2=2V1
объем конуса после изменений увеличился в 2 раза.
2. h=H/3 r=R/3
V2=πr²h/3
V2=π(R/3)²(H/3)/3= πR²H/81 - объем конуса после изменений
V1/V2=πR²H/3 : πR²H/81 = 81/2
V1/V2=27
V2=V1/27
объем конуса уменьшился в 27раз
ответ: 1. объем конуса увеличился в 2р
2. объем уменьшился в 27р