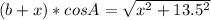
Как известно, сумму углов многоугольника находят по формуле:
180° · (n - 2), где n - число сторон многоугольника.
Сумма углов правильного пятиугольника равна:
180° · (5 - 2) = 180° · 3 = 540°.
Т.к. у правильного пятиугольника все углы равны, то один его внутренний угол равен 540° : 5 = 108°.
Построение правильного пятиугольника (см. рисунок)
1. Строим окружность произвольного радиуса.
2. Строим два перпендикулярных диаметра этой окружности (одна из простейших задач на построение с циркуля и линейки).
3. Делим один из радиусов пополам. Получаем точку А.
4. Измеряем расстояние АВ и строим точку С.
5. Строим окружность этого же радиуса АВ с центром в точке В.
6. Получаем точки D и G.
7. Из точек D и G строим окружности этого же радиуса и получаем точки Е и F.
8. Соединяем точки В, D, Е, F, G - получаем правильный пятиугольник.
Построение перпендикулярных прямых (деление отрезка пополам)
1. Строим один из диаметров.
2. Строим окружности большего (или меньшего) радиуса с центрами в концах построенного диаметра.
3. Соединяем точки пересечения построенных окружностей.
4. Полученная прямая и есть прямая, перпендикулярная данной (и делящая данный отрезок пополам) – в нашем случае, перпендикулярная диаметру.
Построение угла в 36° - см. рисунок
Задача решена.
Рассмотрим ∆ ВОа и ВОе. Они прямоугольные , имеют общую гипотенузу ВО и по равному острому углу при В.
Если гипотенуза и прилежащий к ней угол одного прямоугольного треугольника соответственно равны гипотенузе и прилежащему углу другого треугольника, то такие треугольники равны. ⇒
катет аО = еО
Аналогично доказывается равенство катетов еО и уО треугольников СОе и СОу.
Отрезки Оа, Ое, Оу равны и как перпендикуляры от точки до прямой, являются расстоянием от О до АВ, до ВС и до AD.
Т.е. О - равноудалена от прямых АВ, ВС и AD, ч.т.д.
Как вариант: Из теоремы:
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон, следует:
Точка О - общая для биссектрис двух углов с общей стороной ВС, следовательно, равноудалена от прямых, содержащих их стороны.
Подробнее - на -