1. Если х- коэффициент пропорциональности, а гипотенуза составлена из отрезков 8 и 6, равна 8+6=14/см/,то катеты тогда 8х и 6х, т.к. биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. По теорем ПИфагора
(8х²)+(6х)²=14²
100х²=14², откуда х=1,4, отрицательный корень не подходит по смыслу задачи. Значит, один катет равен 8*1,4=11,2 см, а другой 1,4*6=8,4см.
2. Медиана, проведенная к гипотенузе, равна ее половине, т.е.
14/2= 7 /см/
3. Высота, проведенная к гипотенузе, может быть найдена, как удвоенная площадь треугольника, деленная на гипотенузу, а площадь найдем как половину произведения катетов, т.е. 11,2*8,4/2=94,08/2=47,04/см²/
Высота, проведенная к гипотенузе, равна
2*47,04/14=47,04/7=6,75/см/
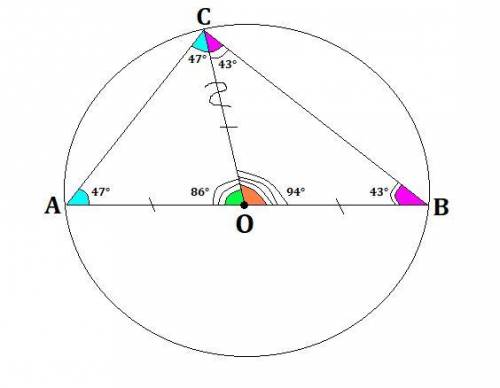
Так как OC и AO - радиусы окружности с центром в точке O ⇒ AO=OC (точки на окружности равноудалены от центра).
Поскольку AO=OC ⇒ ΔAOC - равнобедренный.
∠CAO=∠ACO=47° (по свойству равнобедренного треугольника).
Сумма углов треугольника равна 180°.
⇒ ∠AOC=180°-(47°+47°)=180°-94°=86°.
Сумма смежных углов равна 180°.
∠AOC смежный с ∠COB ⇒ ∠COB=180°-86°=94°.
Так как CO и OB - радиусы окружности с центром в точке O ⇒ CO=OB (точки на окружности равноудалены от центра).
Поскольку CO=OB ⇒ ΔCOB - равнобедренный.
∠OCB=∠CBO (по свойству равнобедренного треугольника) ⇒ их сумма равна 180°-94°=86°, а каждый из них по 43°.
Также можно было найти ∠OCB и ∠CBO по-другому:
Вписанный угол, который опирается на полуокружность, равен 90°.
∠ACB=90°, так как он вписанный (он же ∠С).
Поскольку ∠ACO=47° ⇒ ∠OCB=90°-47°=43°.
Так как ΔCOB - равнобедренный ⇒ ∠OCB=∠CBO (он же ∠B) =43° (по свойству равнобедренного треугольника).
ответ: 43°; 90°.
Объяснение:
1) длины сторон АВ АС ВС
считаются по формуле
Давайте рассмотрим на примере АВ.
А(1;5) В(2;-4)
АВ=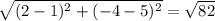
2) уравнение прямой, проходящей через две точки с координатами А(х1,у1) и В(х2, у2) находится по формуле
Подставляем наши значения
-9x+6=y
коэффициенты прямой k1=-9, b1=6
Проделав то же самое, но для прямой по координатам отрезка АС найдем
у=4х+1 , k2=4, b1=1
3) зная два уравнения прямых мы сможем найти угол, которые они образуют при пересечении
tgα=13/35 ⇒ arctg13/35 ≈ 20°
3) УРАВНЕНИЕ ВЫСОТЫ, проведенной через вершину С
Прямая, к которой проведен перпендикуляр описывается уравнением -9x+6=y
k1=-9
Для двух ⊥-ых прямых должно выполняться условие k1*k2=1
т/е подбираем коэффициент k2 для уравнения высоты, поскольку высота треугольника это перпендикуляр, опущенный из вершины. Несложно догадаться, что k2 будет -1/9
Прямая, проходящая через точку N0 (х0, у0)( в нашем случае это С (0, 1) описывается уравнением:
или