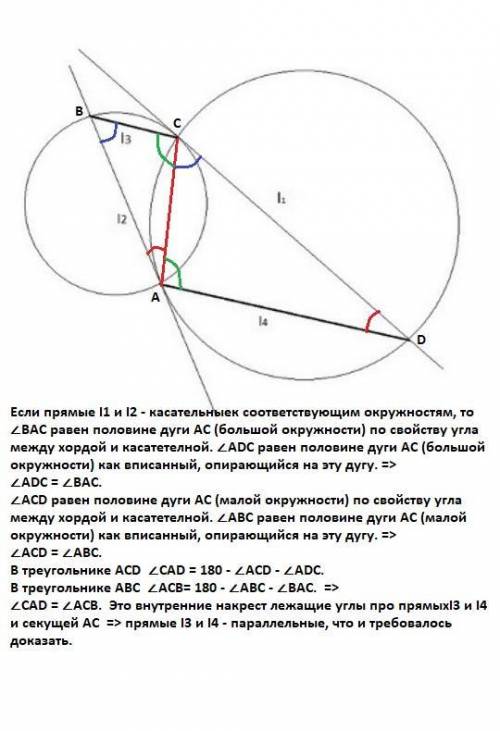
Доказательство в объяснении и приложении.
Объяснение:
Если прямые I1 и I2 - касательные к соответствующим окружностям, то ∠ВАС равен половине дуги АС (большой окружности) по свойству угла между хордой и касательной. ∠ADC равен половине дуги АС (большой окружности) как вписанный, опирающийся на эту дугу. =>
∠АDC = ∠ВАC.
∠ACD равен половине дуги АС (малой окружности) по свойству угла между хордой и касательной. ∠AВC равен половине дуги АС (малой окружности) как вписанный, опирающийся на эту дугу. =>
∠АСD = ∠ABC.
В треугольнике ACD ∠CАD = 180 - ∠АСD - ∠ADC.
В треугольнике AВC ∠АСВ= 180 - ∠АBC - ∠BAC. =>
∠CАD = ∠АСВ. Это внутренние накрест лежащие углы про прямыхI3 и I4 и секущей АС => прямые I3 и I4 - параллельные, что и требовалось доказать.
По условию
ВД = 8, КД = ВД/2 = 4
ИК = ИЕ = 6
--- 1 ---
ΔГКД ~ ΔГЕИ, т.к. угол Г общий и углы К и Е - прямые
Из подобия треугольников
ГД/ГК = ГИ/ГЕ
x/y = (y+6)/(x+4)
x² + 4x = y² + 6y
--- 2 ---
по т. Пифагора для ΔГКД
ГД² = ГК² + КД²
x² = y² + 4²
--- 3 ---
Решаем совместно уравнения из 1 и 2
Вычтем из второго первое
4² + 4x = 6y
x = 3/2*y - 4
Подставим выражение для х во второе
(3/2*y - 4)² = y² + 16
9/4 *y² - 2*3/2*4*y + 16 = y² + 16
5/4*y² - 12y = 0
5y² - 48y = 0
y(5y - 48) = 0
Плохое решение y=0 отбросим
Хорошее решение
y = 48/5
x = 3/2*y - 4 = 3/2*48/5 - 4 = 72/5 - 4 = 52/5
--- 4 ---
ΔГКД ~ ΔГЖЗ
ЖЗ/КД = ГЗ/ГК
z/4 = (y + 6 + 6)/y
z = 4*(y + 12)/y = 4*(48/5 + 12)/(48/5) = 5/12*(48/5 + 12) = 4 + 5 = 9
Нижнее основание трапеции
2z = 2*9 = 18
--- 5 ---
Площадь - половина произведения суммы основания на высоту
S = 1/2*(8 + 18)*12 = 6*26 = 156